1、计算题  如图所示，光滑水平面AB与竖直面内的半圆形导轨在B点相接，导轨半径为R.一个质量为m的物体将弹簧压缩至A点后由静止释放，在弹力作用下物体获得某一向右速度后脱离弹簧，当它经过B点进入导轨瞬间对导轨的压力为其重力的7倍，之后向上运动恰能完成半个圆周运动到达C点．不计空气阻力.

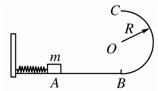
试求：
(1)当m在A点时，弹簧的弹性势能的大小；
(2)物块m从B点运动到C点克服阻力做的功的大小；
（3）如果半圆形轨道也是光滑的，其他条件不变，当物体由A经B运动到C，然后落到水平面，落点为D（题中D点未标出，且水平面足够长），求D点与B点间距离。

参考答案：（1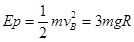）（2）（3）

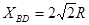
本题解析：（1）物块在B点时，由牛顿第二定律得：
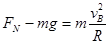?（2分）

在物体从A点到B点的过程中，根据机械能守恒定律，弹簧的弹性势能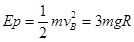? (2分)
（2）物体到达C点仅受重力mg，根据牛顿第二定律有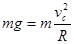?（2分）?
物体从B点到C点只有重力和阻力做功，根据动能定理有：，解得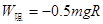
物块m从B点运动到C点克服阻力做的功的大小为?（2分）
（3）在物体从B点到C点的过程中，根据动能定理有：
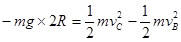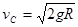，解得??（2分）
由C点到D点，物体做平抛运动，有：
水平方向：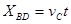
竖直方向：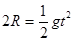
解得：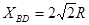
点评：当物体在做曲线运动时，并且涉及的过程比较多，则使用动能定理可以简便解题过程

本题难度：一般

2、简答题  如图所示，长木板A上右端有一物块B，它们一起在光滑的水平面上向左做匀速运动，速度v0=2.0m/s．木板左侧有一个与木板A等高的固定物体C．已知长木板A的质量为mA=1.0kg，物块B的质量为mB=3.0kg，物块B与木板A间的动摩擦因数μ=0.5，取g=10m/s2．
（1）若木板A足够长，A与C第一次碰撞后，A立即与C粘在一起，求物块B在木板A上滑行的距离是多少；
（2）若木板A足够长，A与C发生碰撞后弹回（碰撞时间极短，没有机械能损失），求第一次碰撞后A、B具有共同运动的速度．

参考答案：（1）A与C碰撞后速度即变为0，而B将继续运动，受摩擦力作用，速度由v0减到0，由动能定理：
μmBgL=12mBv20
解得：L=0.40m．
故物块B在木板A上滑行的距离为：L=0.40m．
（2）A与C发生弹性碰撞后，速度大小仍为v0，方向相反，以A、B为研究对象，设A、B有共同的速度v，水平方向不受外力作用，系统动量守恒，设向左为正，有：
mBv0-mAv0=（mA+mB）v
所以：v=(mB-mA)v0mA+mB=v02=1?m/s，方向水平向左．
故第一次碰撞后A、B具有共同运动的速度为1m/s，方向水平向左．

本题解析：

本题难度：一般

3、计算题  把质量为0.5Kg的石块从某高处以30o角斜向上方抛出，初速度是Vo=5m/s，落地速度为V1=15m/s（不计空气阻力）

（1）抛出时，人对石块做了多少功？
（2）抛出点的高度h为多大？

参考答案：（1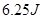）（2）h=10m

本题解析：(1)人对石块做的功等于其动能增加量，故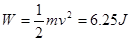?(5分)
（2）石块在抛出后，只有重力做功，根据动能定理可得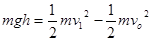：?解得h="10m" ?(5分)
点评：关键是知道抛出石块后，人与石块之间没有力的作用，

本题难度：简单

4、选择题  NBA篮球赛非常精彩，吸引了众多观众．偶尔有这样的场面：在临终场O．1 s的时候，运动员把球投出且准确命中，获得比赛的胜利．如果运动员投篮过程中篮球离开手时速度为v，出手高度为h1，篮筐距地面高度为h2，球的质量为m，空气阻力不计，则篮球进筐时的动能为? (? )
A．mv?/2+mgh1-mgh2
B．mv?/2+mgh2-mgh1
C．mgh1+mgh2- mv?/2
D．mgh2-mgh1- mv?/2

参考答案：A

本题解析：本题考查的是对动能定理的应用问题。由动能定理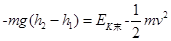：，可知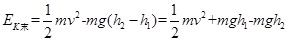：；答案选A。

本题难度：一般

5、计算题  （10分）某物体放在一倾角为θ的斜面上，向下轻轻一推，它刚好能匀速下滑．若给此物体一个沿斜面向上的初速度v0，那么，

（1）物体与斜面间的动摩擦因数μ为多大？
（2）它能沿斜面向上滑的最大位移为多少？

参考答案：;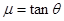

本题解析：依题意物体刚好能匀速下滑，说明：……（2分）
得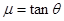……（2分）
向上滑时，受力分析得：物体合外力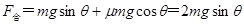……（2分）
依动能定理有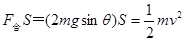：……（2分）
得：……（2分）
本题考查受力分析，当物体匀速下滑时，物体所受重力沿斜面向下的分力等于沿斜面向上的摩擦力，可求出动摩擦因数，当斜面沿斜面上滑时物体所受重力沿斜面向下的分力和摩擦力提供加速度，由牛顿第二定律可求得合外力，再由动能定理可求得位移大小

本题难度：一般