1、简答题  如图所示，轻绳绕过轻滑轮连接着边长为L的正方形导线框A1和物块A2，线框A1的电阻为R，质量为M，物块A2的质量为m（M>m），两匀强磁场区域I、II的高度也为L，磁感应强度均为B，方向水平与线框平面垂直。线框ab边距磁场边界高度为h。开始时各段绳都处于伸直状态，把它们由静止释放，ab边刚穿过两磁场的分界线CC／进入磁场II时线框做匀速运动。求：
（1）ab边刚进入磁场I时线框A1的速度v1；
（2）ab边进入磁场II后线框A1其重力的功率P；
（3）从ab边刚进入磁场II到ab边刚穿出磁场II的过程中，线框中产生的焦耳热Q。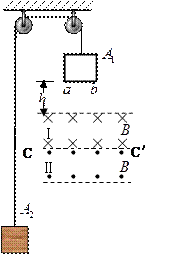

参考答案：
（1）

（2）

（3）

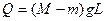
本题解析：（1）由机械守恒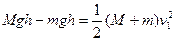：?①? 2分
解得：?②? 1分
（2）设线框ab边进入磁场II时速度为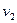，则线框中产生的电动势：?
?③? 1分
线框中的电流?④? 1分
线框受到的安培力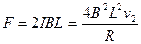?⑤? 2分
设绳对A1、A2的拉力大小为T则：
对A1：T+F=Mg?⑥? 1分
对A2：T="mg?" ?⑦? 1分
联立⑤⑥⑦解得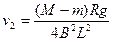：?⑧? 2分
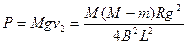?⑨? 2分
（3）从ab边刚进入磁场II到ab边刚穿出磁场II的此过程中线框一直做匀速运动，根据能量守恒得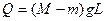：?⑩? 2分

本题难度：一般

2、计算题  如图所示，一电子以速度1.0×107m/s与x轴成30°的方向从原点出发，在垂直纸面向里的匀强磁场中运动，磁感应强度B=1T。那么圆运动的半径为多少？经过多少时间第一次经过x轴。（电子电量e＝－1.6×10-19 C，电子质量m＝9.1×10-31 kg）

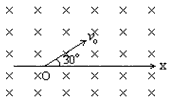
参考答案：5.7×10-5 m，5.95×10-12 s

本题解析：

本题难度：一般

3、计算题  （10分）如图所示，MN表示真空室中垂直于纸面放置的感光板，它的一侧有匀强磁场，磁场方向垂直于纸面向里，磁感应强度大小为B. 一个电荷量为q的带电粒子从感光板上的狭缝O处以垂直于感光板的初速度v射入磁场区域，经一次偏转到达P点. 经测量P、O间的距离为l，不计带电粒子受到的重力. 求：

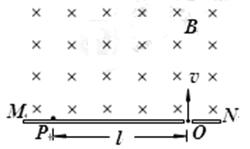
（1）带电粒子所受洛伦兹力的大小；
（2）带电粒子的质量。

参考答案：（1）（2）

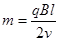
本题解析：（1）带电粒子在磁场中所受洛伦兹力? 2分
（2）带电粒子在磁场中做匀速圆周运动，设其半径为R，由牛顿第二定律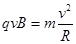?2分
带电粒子做匀速圆周运动的半径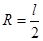? 2分
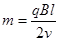解得 ?2分

本题难度：一般

4、简答题  如图所示，再第二象限和第四象限的正方形区域内分别存在着面积相同的匀强磁场，磁感应强度均为B，方向相反，且都垂直与xoy平面；在第一象限内存在着平行与xoy平，沿x轴方向的匀强磁场（图中没有画出）；一电子由P（-d，d）点，沿x轴正方向射入磁场区域Ⅰ．（电子质量为m，电荷量为e，sin53°=0.8）
（1）若电子离开磁场区域Ⅰ后直接进入第三象限，求入射速度的范围；
（2）若电子从（0，

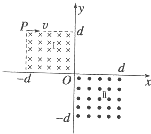
参考答案：（1）电子能从第三象限射出的临界轨迹如图甲所示．

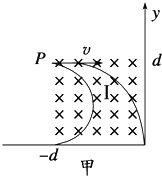
由几何知识可知，电子偏转半径范围为：d2＜r＜d，
电子在匀强磁场中做匀速圆周运动，由牛顿第二定律得：evB=mv2r，
解得，电子入射速度的范围为：eBd2m＜v＜eBdm．
（2）电子运动轨迹如图所示：

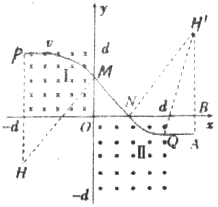
电子从（0，d2）位置射出设电子在磁场中运动的轨道半径为R，由几何知识可得：
R2=（R-d2）2+d2，
解得：R=5d4，
由牛顿第二定律得：evB=mv20R，
由几何关系得进入电场与水平方向的夹角为53°；
进入电场以后带电粒子垂直于x轴进入磁场Ⅱ，
知粒子在电场中做逆向平抛，根据平抛的规律：
带点粒子沿y轴方向的速度为：vy=v0sin53°=0.8v0，
带点粒子沿x轴方向的速度为：vx=v0cos53°=0.6v0，
根据位移的关系可以求得：E=3edB22m，方向沿x轴的正方向；
（3）根据粒子在电场中沿x轴运动规律：x=12at2，
则在磁场区域Ⅱ位置的横坐标为316d，
磁场区域Ⅱ，由牛顿第二定律得：evB=mv2r，
由几何知识可得：r=d，r2=（316d）2+y2，
解得：y=

本题解析：

本题难度：一般

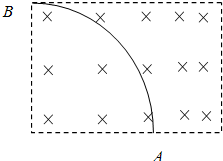
5、选择题  一个重力不计的带电粒子垂直射入自左向右逐渐增强的磁场中，由于周围气体的阻碍作用，其运动轨迹恰为一段圆弧，则从如图所示中可以判断（　　）
A．粒子从A点射入，速率逐渐减小
B．粒子从A点射入，速率逐渐增大
C．粒子从B点射入，速率逐渐减小
D．粒子从B点射入，速率逐渐增大