1、简答题  质谱仪的装置如图，假设从离子源S出来的离子质量为m，电量为q，初速度为零，被电压为U的电场加速后进入磁感应强度为B的匀强磁场中，最后到达平板MN上的P点．已知P到O的距离l，不计重力，求粒子的电荷q与质量m之比．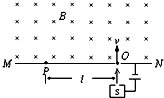

2、计算题  如图所示，y轴上A点距坐标原点的距离为L，坐标平面内有边界过A点和坐标原点O的圆形匀强磁场区域，磁场方向垂直坐标平面向里。有一电子（质量为m、电荷量为e）从A点以初速度v0沿着x轴正方向射入磁场区域，并从x轴上的B点射出磁场区域，此时速度方向与x轴正方向之间的夹角为60°。求：

（1）磁场的磁感应强度大小；（2）电子在磁场中运动的时间。

3、计算题  如图所示，空间区域I、II有匀强电场和匀强磁场，MN、PQ为理想边界，I区域高度为d，II区域的高度足够大，匀强电场方向竖直向上；I、II区域的磁感应强度大小均为B，方向分别垂直纸面向里和向外。一个质量为m、带电荷量为q的小球从磁场上方的O点由静止开始下落，进入场区后，恰能做匀速圆周运动。已知重力加速度为g。

(1)试判断小球的电性并求出电场强度E的大小；
(2)若带电小球运动一定时间后恰能回到O点，求它释放时距MN的高度h；
(3)试讨论在h取不同值时，带电小球第一次穿出I区域的过程中，电场力所做的功。

4、计算题  某学习小组到大学的近代物理实验室参观，实验室的老师给他们提供了一张经过放射线照射的底片，底片上面记录了在同一直线上的三个曝光的痕迹，如图所示。老师告诉他们，实验时底片水平放置，第2号痕迹位置的正下方为储有放射源的铅盒的开口，放射源可放射出α、β、γ三种射线。然后又提供了α、β、γ三种射线的一些信息如下表。已知铅盒上的开口很小，故射线离开铅盒时的初速度方向均可视为竖直向上，射线中的粒子所受重力、空气阻力及它们之间的相互作用力均可忽略不计，不考虑粒子高速运动时的相对论效应。
原子质量单位1u=1.66×10-27 kg，元电荷e=1.6×10-19 C，光速c=3.0×108m/s。
?
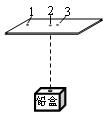（1）学习过程中老师告诉同学们，可以利用三种射线在电场或磁场中的偏转情况对它们加以辨别。如果在铅盒与底片之间加有磁感应强度B=0.70T的水平匀强磁场，请你计算一下放射源射出α射线在此磁场中形成的圆弧轨迹的半径为多大？（保留2位有效数字）
（2）老师对如图所示的“三个曝光的痕迹”解释说，底片上三个曝光的痕迹是铅盒与底片处在同一平行于三个痕迹连线的水平匀强电场中所形成的。
①试分析说明，第2号痕迹是什么射线照射形成的；
②请说明α粒子从铅盒中出来后做怎样的运动；并通过计算说明第几号曝光痕迹是由α射线照射形成的。

5、简答题  一个负离子，质量为m，电量大小为q，以速率V垂直于屏S经过小孔O射入存在着匀强磁场的真空室中(如图11)。磁感应强度B的方向与离子的运动方向垂直，并垂直于图1中纸面向里。

(1)求离子进入磁场后到达屏S上时的位置与O点的距离。
(2)如果离子进入磁场后经过时间t到达位置P，证明:直线O与离子入射方向之间的夹角θ跟t的关系是。