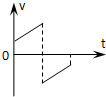
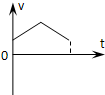
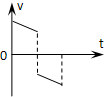
1、选择题  从手中竖直向下抛出的小球，与水平地板碰撞后又弹回到手中，小球与水平地板碰撞时间极短．若不计空气阻力和碰撞过程中动能的损失，则下列能够描述小球从抛出到弹回手中整个过程的速度-时间图象是（　　）
A．

B．

C．

D．

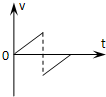
参考答案：小球以初速度v0竖直向下抛出，先向下做匀加速直线运动，速度为正值；与地面碰撞后，速度突然反向，变为负值，向上做匀减速直线运动．只有A符合小球运动情况．故A正确．
故选A

本题解析：

本题难度：简单

2、选择题  已知做匀加速直线运动的物体第2s末速度为4m/s，则物体
[? ]
A．加速度一定为2m/s2
B．前4s内位移一定为16m
C．前2s内位移可能是2m
D．前4s内位移可能为32m

参考答案：B

本题解析：

本题难度：一般

3、选择题  不定项选择
一物体位移与时间的关系为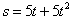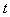（以秒为单位，以米为单位）（ ? ）
A．物体的初速度为2.5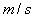
B．物体的加速度是10
C．物体的初速度是10
D．物体的加速度是5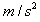

参考答案：B

本题解析：

本题难度：简单

4、简答题  一辆警车停在公路边值勤，警员突然发现从他旁边以10m/s的速度匀速行驶的货车严重超载，他决定前去追赶，经过5.5s后警车发动起来，并以2.5m/s2的加速度做匀加速运动，但警车的行驶速度必须控制在90km/h以内．试求：
（1）警车在追赶货车的过程中，两车间的最大距离是多少；
（2）警车发动后要多长时间才能追上货车．

参考答案：（l）当两车速度相等时，它们间的距离最大
设警车发动后经过t1时间两车的速度相等．
则：t1=v1a=102.5=4s　　　　　　　　　　　　　
货车的位移：s货=（5.5+4）×10m=95m　　
警车的位移s警=12at12=12×2.5×42m=20m
所以两车间的最大距离△s=s货-s警=75m
（2）警车刚达到最大速度用的时间为　　t=va=10s　　　　　
s′货=（5.5+10）×10m=155m
s′警=12at22=12×2.5×102m=125m
因为s′货＞s′警，故此时警车尚未赶上货车，且此时两车距离
△s′=s′货-s′警=30m
警车达到最大速度后做匀速运动，设再经过△t时间追赶上货车，则
△t=△s′v0-v=2s
所以警车发动后要经过t=t2+△t=12s才能追上货车．
答：（1）警车在追赶货车的过程中，两车间的最大距离是75m；（2）警车发动后要12s才能追上货车．

本题解析：

本题难度：一般

5、选择题  一物体从静止开始做匀加速直线运动，加速度大小为5m/s2，那么前2s内与前4s内汽车通过的位移之比为（　　）
A．1：1
B．1：4
C．3：4
D．4：3

参考答案：物体从静止开始做匀加速直线运动，初速度为零，故位移时间关系公式可以简化为：x=12at2；
那么前2s内与前4s内汽车通过的位移之比为：x2x4=(t2t4)2=14；
故选B．

本题解析：

本题难度：简单