1、简答题  一辆汽车以72km/h的速率在某郊区匀速行驶，当这辆违章超速行驶的汽车刚刚驶过一辆警车时，警车立即从静止以2m/s2的加速度匀加速追去．
（1）警车何时能截获超速汽车？警车截获超速汽车时，警车的速度为多大？
（2）在追上前，警车和汽车何时相距最远？最远距离是多少？

参考答案：（1）已知v汽=72km/h=20m/s，
设经过时间?t?两车相遇，则有
S警=S汽
即12at2=vt
代入数据解得t=20s?
此时警车的速度：v警=at=2×20m/s=40m/s?
（2）在追赶过程中，
当警察的速度小于汽车的速度时，两车之间的距离仍在继续增大；
当警察的速度大于汽车的速度时，甲、乙之间的距离便不断减小；
当v警=v汽时，两车相距最远
即v警=at′=v汽
∴t′=v汽a=202s=10s
即10s末两车之间距离最大
且：△Snax=v汽t′-12at′2=20×10m-12×2×102m=100m
答：20s时警车追上超速汽车，此时警车的速度为40m/s，当10s时，两车相距最远，最远距离为100m．

本题解析：

本题难度：一般

2、简答题  甲、乙两车在一条直线上沿相同方向运动，甲在乙前x=56m处，甲以初速度v1=16m/s、加速度大小为a1=2m/s2匀减速刹车，乙以初速度v2=4m/s、加速度大小为a2=1m/s2做匀加速运动，求：
（1）乙车追上甲车前二者间的最大距离；
（2）乙车追上甲车所需时间．

参考答案：（1）在开始阶段甲车在前、乙车在后，且甲车速度比乙车大，两车距离一直增大，设运动时间为?t?时速度相同，设为v，
应用速度公式v=v0+at，有v1-a1t=v2+a2t
代入数据解得t=4s，v=v1-a1t=8m/s．
此后甲车减速、乙车还在加速，两车距离缩短，所以在速度相等时两车距离最大，
最大距离为△x=x+x1-x2=56m+v2-v12-2a1-v2-v222a2=80m．
（2）甲车停下还需时间为t2=0-v-a1=4s，运动位移为x3=0-v2-2a1=16m．
在此时间内乙车位移为x4=vt2+12a2t22=40m．
显然此时乙车还没有追上甲车，此后甲车停止运动，设乙车追上甲车需时间为t1，则有x+0-v12-2a1=v2t1+12a2t12
联立解得t1=12s．
答：（1）乙车追上甲车前二者间的最大距离为80m．
（2）乙车追上甲车所需时间为12s．

本题解析：

本题难度：一般

3、简答题  如图所示，传送带与水平方向成θ=30°角，皮带的AB部分长为L=3.25m，皮带以速度v=2m/s顺时针方向运动，在A端无初速地放上一质量为m=1kg的小物体，小物体与皮带间的动摩擦因数为μ=

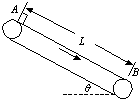
参考答案：（1）第一阶段：物体沿传送带向下做匀加速直线运动，则由牛顿第二定律得
? mg?sin30°+μmg?cos30°=ma1，
得加速度为? a1=8?m/s2，
设加速到与传送带同速的时间为t1：v=a1t1
则得t1=0.25?s，
此过程物体的位移为 s1=0.25?m，皮带位移为s1′=vt1=0.5?m．
第二阶段：由于mgsinθ＞μFN=μmgcosθ，故物体继续沿传送带向下做匀加速直线运动
则有? mg?sin30°-μmg?cos30°=ma2，
得加速度为 a2=2?m/s2，
此过程通过的位移? s2=（3.25-0.25）m=3?m，
由s2=vt2+12a2t22，解得：t2=1?s，
总时间为t=t1+t2=1.5?s，皮带位移为s2′=vt2=2?m，
（2）从A到B运动的过程中一共产生的热量为? Q=f△s1+f△s2=f（s1′-s1）+f（s2′-s2）=3.75?J．
答：
（1）物体从A端到B端所需的时间是1.5s，
（2）从A到B运动的过程中一共产生3.75J的热量．

本题解析：

本题难度：一般

4、选择题  美国“肯尼迪号”航空母舰上有帮助飞机起飞的弹射系统，已知“F-Al5”型战斗机在跑道上加速时产生的加速度为4.5m/s2，起飞速度为50m/s．若该飞机滑行100m时起飞，则弹射系统必须使飞机具有的初速度为（　　）
A．30m/s
B．10m/s
C．20m/s
D．40m/s

参考答案：设飞机的初速度为v0，已知飞机的加速度a、位移x、末速度v，此题不涉及物体运动的时间，
由匀变速直线运动的位移时间公式：v2-v20=2ax
解得：v0=40m/s
故选：D

本题解析：

本题难度：简单

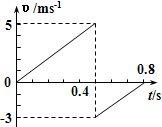
5、选择题  小球在t=O时刻从空中自由下落，与水平地面相碰后弹到空中某一高度，其速度-时间图象如图所示，则由图可知（　　）
A．小球下落的最大速度为5m/s
B．小球下落的最大速度为3m/s
C．小球能弹起的最大高度为0.45m
D．小球能弹起的最大高度为1.25m