1、简答题 在如图所示的空间区域里,x轴下方有一匀强电场,场强方向跟x轴负方向成60°角,大小为E=
×105N/C,x轴上方有一垂直纸面向里的匀强磁场,有一质子以速度υ=2.0×106m/s由x轴上A点(OA=20cm)从与x轴正方向成30°角射入磁场,恰好从坐标原点O穿过x轴射入电场,已知质子质量m=1.6×10-27kg,求
(1)匀强磁场的磁感应强度;
(2)质子经过电场后,再次射入磁场的位置和方向.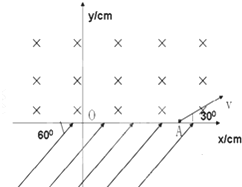
参考答案:(1)画出质子在磁场中运动的轨迹如图所示,由几何知识得
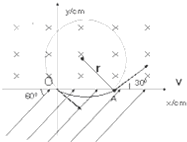
轨迹半径r=OA=20cm=0.2m.
由qvB=mv2r得,
B=mvqr=0.1T
(2)由图看出,质子进入电场时速度方向与电场方向垂直,做类平抛运动,则
沿电场线方向? s1=12?qEmt2
垂直电场线方向 s2=vt
几何关系:s1s2=tan30°
联立可得:t=
本题解析:
本题难度:一般
2、选择题 在一次汽车拉力赛中,汽车要经过某半径为R的圆弧形水平轨道,地面对汽车的最大静摩擦力为车重的0.2倍,汽车要想通过该弯道时不发生侧滑,那么汽车的行驶速度不应大于( )
A.
B.gR
C.
D.
参考答案:根据fm=0.2mg=mv2R得,v=
本题解析:
本题难度:一般
3、计算题 长为L的轻杆一端安在光滑固定转动轴O上,另一端固定有一只质量为m的小球A(视为质点)。给小球一个初速度,使它在竖直面内绕O做圆周运动,已知:当小球到达最高点时,小球对杆的压力大小为小球重力的1/4;小球通过最低点时速度大小为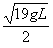 。求: 。求:
(1)小球通过最高点时的速率V。
(2)小球通过最低点时对杆的拉力大小F。
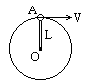
参考答案:解:(1)小球在最高点的受力如图:小球在最高点的向心力由mg和N的合力来提供,由牛顿第二定律得
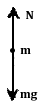
mg-N=m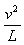
N=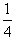 mg mg
解得:v=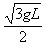
(2)小球在最低点时,杆对小球的拉力为F′,受力如图。同理由牛顿第二定律得:
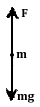
F′-mg=m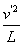
v"=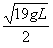
得:F′=5.75mg
由牛顿第三定律可知,小球对杆的拉力大小F=5.75mg
本题解析:
本题难度:一般
4、简答题 现根据对某一双星系统的光学测量确定,该双星系统中每个星体的质量都是M,两者相距L,它们正围绕两者连线的中点做圆周运动.万有引力常量为G.求:
(1)试计算该双星系统的运动周期T.
(2)若实验上观测到运动周期为T’,且Tn:T=1: (N>1),为了解释两者的不同,目前有一种流行的理论认为,在宇宙中可能存在一种望远镜观测不到的物质--暗物质,作为一种简化的模型,我们假定在以这两个星体连线为直径的球体内均匀分布着这种暗物质,而不考虑其他暗物质的影响,试根据这一模型和上述观测结果确定该星系间这种暗物质的密度.
参考答案:(1)由万有引力提供向心力有:GM2L2=M?L2?4π2T2? ①
解得T=πL
本题解析:
本题难度:一般
5、选择题 下列关于向心力的论述中正确的是
[? ]
A.物体因为受到向心力 的作用,才可能做圆周运动? 的作用,才可能做圆周运动?
B.向心力仅仅是从它产生的效果来命名的,它可以使有初速 度的物体做圆周运动,它的方向始终指向圆心 度的物体做圆周运动,它的方向始终指向圆心
C.向心力可以是重力、弹力、摩擦力中的某一种力,也可以是这些力中某几个力的合力
D.向心力只改变速度的方向,不改变速度的大小
参考答案:ABCD
本题解析:
本题难度:简单
|
|