1、计算题  （10分）如图所示，长木板A上右端有一物块B，它们一起在光滑的水平面上向左做匀速运动，速度v0=2m/s。木板左侧有一个与木板A等高的固定物体C。已知长木板A的质量为mA=1.0kg，物块B的质量为mB=3.0kg，物块B与木板A间的动摩擦因数μ=0.5，取g=10m/s2。

（1）若木板A足够长，A与C第一次碰撞后，A立即与C粘在一起，求物块 B在木板A上滑行的距离L应是多少；
（2）若木板足够长，A与C发生碰撞后弹回（碰撞时间极短，没有机械能损失），求第一次碰撞后A、B具有共同运动的速度v；
（3）若木板A长为0.48m，且A与C每次碰撞均无机械能损失，求A与C碰撞几次，B可脱离A？

参考答案：（1）0.40m?（2）1 m/s?（3）第二次碰后B可脱离A板

本题解析：（1）A与C碰撞后速度即变为0，而B将继续运动，受摩擦力作用，速度由v0减到0，由动能定理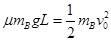
L=0.40m?（2分）
（2）A与C发生弹性碰撞后，速度大小仍为v0，方向相反，以A、B为研究对象，设A、B有共同的速度v，水平方向不受外力作用，系统动量守恒，设向左为正

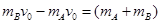
v=1 m/s ，方向水平向左?（3分）
（3）第一次A与C碰后，A、B有共同的速度v，B在A上相对于A滑行L1，则

L1=0.40m?（2分）
第二次A与C碰后至A、B有共同的速度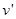，B在A上相对于A滑行L2，则


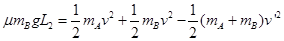
由以上两式，可得L2=0.10m?（2分）
则L1+ L2=0.5m＞0.48m
即第二次碰后B可脱离A板?（1分）

本题难度：一般

2、计算题  如图甲所示，在倾角为30°的足够长光滑斜面AB前，有一粗糙水平面OA，OA长为4 m．有一质量为m的滑块，从O处由静止开始受一水平向右的力F作用．F按图乙所示的规律变化．滑块与OA间的动摩擦因数μ＝0.25，g取10 m/s2，试求：

（1）滑块到A处的速度大小；
（2）不计滑块在A处的速率变化，滑块冲上斜面AB的长度是多少？
（3）假设水平面足够长，且与滑块间的动摩擦因数不变则滑块最终停在距A多远的水平面上？

参考答案：(1)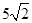m/s? (2) 5m? (3)10m

本题解析：（1）0-2m过程中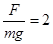，即，做功
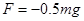2-3m过程中，即,做功
3-4m过程中，F=0，不做功，
整个过程中摩擦力做功为
根据动能定理可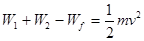得，解得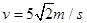
（2）根据机械能守恒定律可得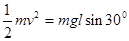：，所以l=5m
（3）根据动能定理可得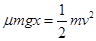，解得x=10m
点评：了解研究对象的运动过程是解决问题的前提，根据题目已知条件和求解的物理量选择物理规律解决问题．一个题目可能需要选择不同的过程多次运用动能定理研究．

本题难度：一般

3、选择题  如图4－2－5所示，电梯质量为M，地板上放置一质量为m的物体．钢索拉电梯由静止开始向上加速运动，当上升高度为H时，速度达到v，则(　　)

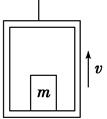
图4－2－5
A．地板对物体的支持力做的功等于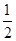mv2
B．地板对物体的支持力做的功等于mgH
C．钢索的拉力做的功等于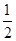Mv2＋MgH
D．合力对电梯M做的功等于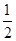Mv2

参考答案：D

本题解析：选D.对物体m应用动能定理：WN－mgH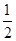＝mv2，故WN＝mgH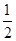＋mv2，A、B均错；以电梯和物体整体为研究对象应用动能定理，钢索拉力做的功WT＝(M＋m)gH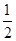＋?(M＋m)v2，故C错误，由动能定理知，合力对电梯M做的功应等于电梯动能的变化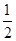Mv2，故D正确．

本题难度：一般

4、选择题  竖直平面内有两个半径不同的半圆形光滑轨道,如图所示,A、M、B三点位于同一水平面上,C、D分别为两轨道的最低点,将两个质量不相同的小球分别从A、B处同时无初速释放,则

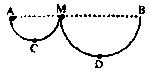
A．通过C、D时,两球的速度大小相等
B．通过C、D时,两球的机械能大小相等
C．通过C、D时,两球的加速度大小相等
D．通过C、D时,两球对轨道的压力大小相等

参考答案：C

本题解析：由动能定理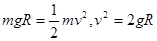，所以最低点速度大小不相等，在运动过程中两球的机械能守恒，在初始位置高度相同，但质量不同，所以重力势能不同机械能不同，B错；在最低点由合外力提供向心力，向心加速度为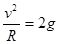，C对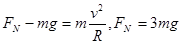；，由于两球质量不同支持力不同，D错；

本题难度：一般

5、简答题  如图所示，质量为m=0.2kg的小物体放在光滑的

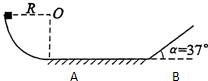
参考答案：已知m=0.2kg，k=0.55m，SAB=1m，m=0.1?α=37°
（1）小物体内圆弧上端到B点的过程中，由动能定理有
mgR?μmgSAB=12mυ2Bθ…（1）
υ2B=2gR-2μgSAB=9…（2）
υB=3m/s…（3）
（2）设物体第一次滑上右侧轨道最大高度为H
此时物体离B点的距离为S，由几何关系有HS=sinα…（4）
由动能定理有-μmgcosα?S-mgH=0-12mυ2B…（5）
将（4）式代入（5）式?有
H=2764≈0.40m
答：（1）物体第一次滑到水平轨道与右侧斜面轨道交接处的速度大小是3m/s
（2）物体第一次滑上右侧斜轨道的最大高度是0.40m

本题解析：

本题难度：一般