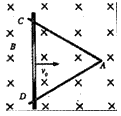
1、选择题  如图所示，光滑金属导轨AC、AD固定在水平面内，并处在方向竖直向下、大小为B的匀强磁场中。有一质量为m的导体棒以初速度v0从某位置开始在导轨上水平向右运动，最终恰好静止在A点。在运动过程中，导体棒与导轨始终构成等边三角形回路，且通过A点的总电荷为Q。已知导体棒与导轨间的接触电阻阻值为R，其余电阻不计，则

[? ]
A. 该过程中导体棒做匀减速运动
B. 该过程中接触电阻产生的热量为
C. 开始运动时，导体棒与导轨所构成回路的面积为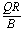
D. 当导体棒的速度为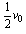时，回路中感应电流大小为初始时的一半

参考答案：C

本题解析：

本题难度：一般

2、选择题  关于感应电流，下列说法中正确的是（?）?
A．只要穿过闭合电路的磁通量不为零，闭合电路中就有感应电流产生?
B．穿过螺线管的磁通量发生变化时，螺线管内就一定有感应电流产生?
C．线圈不闭合时，即使穿过线圈的磁通量发生变化，线圈中也没有感应电流?
D．只要闭合电路在磁场中做切割磁感线运动，电路中就一定有感应电流产生

参考答案：C

本题解析：只要穿过闭合电路的磁通量发生变化，闭合电路中就有感应电流产生，A错；同理可知，只有电路闭合才有可能产生感应电流，B错；C对；只有闭合电路的一部分导体在磁场中做切割磁感线运动，电路中才有感应电流产生，D错；
点评：难度较小，产生感应电流有两种方式：切割和磁通量发生变化，首先电路必须闭合

本题难度：简单

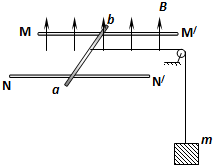
3、简答题  如图为一电梯简化模型，导体棒ab架在水平导轨上，导轨间加有竖直向上的匀强磁场，磁感应强度B=10T．导体棒ab通过轻质细绳与电梯箱体相连，所有摩擦都不计，已知ab棒的长度为l=10m，质量不计，通过的电流大小为I，电梯箱体质量为m=100km，求：
（1）为了能提起电梯箱体，导体棒ab中的电流方向应朝哪？大小至少为多少？
（2）现使导体棒以恒定的功率P（即安培力的功率）从静止运行，试通过列式分析ab棒中电流的大小如何变化？
（3）若在题（2）中P=5000W，电梯箱体上升h=1m高度时，运行达到稳定状态，则此过程电梯运行的时间为多少？

参考答案：（1）因为安培力的方向水平向左，根据左手定则知，导体棒中的电流方向为：b到a．
根据BIl≥mg，得：I≥mgBl=10A．
（2）BIl-mg=ma，P=BIlv
因为v在增大，而功率P不变，所以I在变小，
当BIl-mg=0时，箱体做匀速直线运动，导体棒中电流保持不变．
（3）当a=0时，BIl-mg=0
得：I=mgBl=10A，
则速度：v=PBIl=Pmg=5m/s．
根据动能定理得：Pt-mgh=12mv2
解得：t=mgh+12mv2P=1000+12505000s=0.45s．
答：（1）为了能提起电梯箱体，导体棒ab中的电流方向b到a，大小至少为10A．
（2）ab棒中的电流先变小后不变．
（3）此过程电梯运行的时间为0.45s．

本题解析：

本题难度：一般

4、选择题  竖直放置的平行光滑导轨，其电阻不计，磁场方向如图所示，磁感强度B=0.5T，导体ab及cd长均为0.2m，电阻均为0.1Ω，重均为0.1N，现用力向上推动导体ab，使之匀速上升（与导轨接触良好），此时，cd恰好静止不动，那么ab上升时，下列说法正确的是（?）

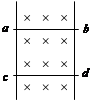
A．ab受到的推力大小为2N
B．ab向上的速度为2m/s
C．在2s内，推力做功转化的电能是0.8J
D．在2s内，推力做功为0.6J

参考答案：B

本题解析：由于ab向上做匀速直线运动时，cd恰好静止不动，即cd受到的安培力F=G=0.1N，由安培力公式F=BIL可计算出电路中的电流为I=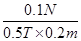=1A，所以ab中的电流也是1A，且方向是由b到a，故ab受到的安培力的方向是竖直向下的，所以ab受到的推力大小为Fab=F安+G=0.1N+0.1N=0.2N，故A是不对的；
ab产生的感应电压应该是E=I（R+R）=1A×0.2Ω=0.2V，所以再由公式E=BLv可得，ab向上的速度为v=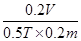=2m/s，故B是正确的；
C中在2s内，推力做功转化的电能是W=EIt=0.2V×1A×2s=0.4J，故C是不正确的；
D中在2s内，推力做功为W′=Pt=Fabvt=0.2N×2m/s×2s=0.8J，故D是不对的。

本题难度：一般

5、选择题  如图所示，金属环半径为a，总电阻为R，匀强磁场磁感应强度为B，垂直穿过环所在平面．电阻为R/2的导体杆AB沿环表面以速度v向右滑至环中央时，杆的端电压为（　　）
A．Bav
B．

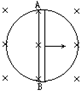
参考答案：导体棒相当于电源，切割产生的感应电动势为E=B?2av
总电阻：R总=R22+R2=3R4
则电流的大小为：I=2Bav3R4=8Bav3R．
所以杆的两端电压为：U=E-I×R2=2Bav3．故C正确，A、B、D错误．
故选：C．

本题解析：

本题难度：简单