1、选择题 下列说法中正确的是,感应电动势的大小( ? )
A.跟穿过闭合电路的磁通量有关系
B.跟穿过闭合电路的磁通量的变化大小有关系
C.跟穿过闭合电路的磁通量的变化快慢有关系
D.跟电路的电阻大小有关系
参考答案:C
本题解析:
本题难度:简单
2、简答题 如图甲所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为0.5m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.质量为0.2kg的导体棒MN垂直于导轨放置,距离顶端1m,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面向下的匀强磁场,磁感应强度随时间变化的规律如图乙所示.先固定导体棒MN,2s后让MN由静止释放,运动一段时间后,小灯泡稳定发光.重力加速度g取10m/s2,sin37°=0.6.求
(1)1s时流过小灯泡的电流大小和方向;
(2)小灯泡稳定发光时消耗的电功率;
(3)小灯泡稳定发光时导体棒MN运动的速度.

参考答案:(1)由图知,△B△t=0.4T/s
根据法拉第电磁感应定律得在0-2s内回路中产生的感应电动势 E=△B△tS=0.82×0.5×1V=0.2V
感应电流的大小 I=ER灯+RMN=0.21+1A=0.1A
根据楞次定律判断可知,回路中电流的方向沿逆时针.
(2)、(3)2s后,当MN棒匀速直线运动时达到稳定状态,设稳定时速度为v.
则产生的感应电动势为 E′=BLv
感应电流 I′=E′R灯+RMN
MN棒所受的安培力大小 F=BI′L,方向沿轨道向上.
联立得:F=B2L2vR灯+RMN
MN棒匀速运动时,受力平衡,则有:F+μmgcos37°=mgsin37°
由上两式得:B2L2vR灯+RMN+μmgcos37°=mgsin37°
将B=0.8T,L=0.5m,R灯=1Ω,RMN=1Ω,μ=0.5,m=0.2kg
代入解得:v=5m/s
则得:I′=E′R灯+RMN=BLvR灯+RMN=0.8×0.5×51+1A=1A
小灯泡稳定发光时消耗的电功率 P=I2R灯=12×1W=1W
答:(1)1s时流过小灯泡的电流大小是0.1A,方向逆时针.(2)小灯泡稳定发光时消耗的电功率是1W.(3)小灯泡稳定发光时导体棒MN运动的速度是5m/s.
本题解析:
本题难度:一般
3、选择题 如图所示,用铝板制成U型框,将一质量为m的带电小球用绝缘细线悬挂在框中,使整体在匀强磁场中沿垂直于磁场方向向左以速度v匀速运动,悬挂拉力为FT,则( )
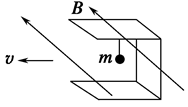
A.悬线竖直,FT=mg
B.悬线竖直,FT>mg
C.悬线竖直,FT<mg
D.无法确定FT的大小和方向
参考答案:A
本题解析:设两板间的距离为L,由于向左运动过程中竖直板切割磁感线,产生动生电动势,由右手定则判断下板电势高于上板,动生电动势大小E=BLv,即带电小球处于电势差为BLv的电场中,所受电场力F电=qE电=q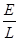 =q
=q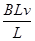 =qvB
=qvB
设小球带正电,则电场力方向向上.同时小球所受洛伦兹力F洛=qvB,方向由左手定则判断竖直向下,即F电=F洛,故无论小球带什么电怎样运动,FT=mg.选项A正确.
本题难度:一般
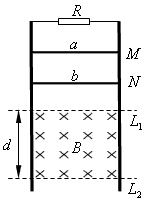
4、计算题 如图所示,电阻忽略不计的、两根两平行的光滑金属导轨竖直放置,其上端接一阻值为3Ω的定值电阻R。在水平虚线L1、L2间有一与导轨所在平面垂直的匀强磁场B,磁场区域的高度为d=0.5m。导体棒a的质量ma=0.2kg、电阻Ra=3Ω;导体棒b的质量mb=0.1kg、电阻Rb=6Ω,它们分别从图中M、N处同时由静止开始在导轨上无摩擦向下滑动,都能匀速穿过磁场区域,且当b刚穿出磁场时a正好进入磁场。设重力加速度为g=10m/s2,不计a、b棒之间的相互作用。导体棒始终与导轨垂直且与导轨接触良好。求:
(1)在整个过程中,a、b两棒分别克服安培力所做的功;
(2)导体棒a从图中M处到进入磁场的时间;M点和N点距L1的高度。
参考答案:解:(1)Wa=magd=1.0J
Wb=mbgd=0.5J
(2)b在磁场中匀速运动时:速度为vb,总电阻R1=7.5Ω
b中的电流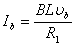 ①
①
由以上各式得: ②
②
同理,a棒: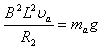 ③
③
由以上各式得,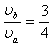 ④
④
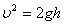 ?⑤
?⑤
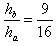 ?⑥
?⑥
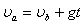 ?⑦
?⑦
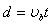 ?⑧
?⑧
由④⑤⑥⑦⑧得Ha=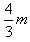 ⑨,Hb=
⑨,Hb=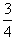 m ⑩
m ⑩
解得导体棒a从图中M处到进入磁场的时间为
本题解析:
本题难度:困难
5、选择题 如图所示,MN、PQ是间距为L的平行金属导轨,置于磁感强度为B,方向垂直导轨所在平面向里的匀强磁场中,M、P间接有一阻值为R的电阻.一根与导轨接触良好、有效阻值也为R的金属导线ab垂直导轨放置,并在水平外力F的作用下以速度v向右匀速运动,则(不计导轨电阻)( )
A.通过电阻R的电流方向为P→R→M
B.ab两点间的电压为BLv
C.a端电势比b端高
D.外力F做的功等于电阻R上发出的焦耳热