1、选择题 如图所示,自由下落的小球,从它接触竖直放置的轻质弹簧开始到弹簧压缩到最短的过程中,小球的加速度和速度的变化情况是?(?)
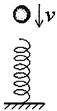
A.加速度变小,速度变小
B.加速度变大,速度变小
C.加速度先变小后变大,速度先变大后变小
D.加速度先变大后变小,速度先变大后变小
参考答案:C
本题解析:略
本题难度:简单
2、计算题 (15分)如图所示,在光滑绝缘水平面上,质量为m的均匀绝缘棒AB长为L、带有正电,电量为Q且均匀分布。在水平面上O点右侧有匀强电场,场强大小为E,其方向为水平向左,BO距离为x0,若棒在水平向右的大小为QE/4的恒力作用下由静止开始运动。求:
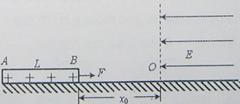
⑴棒的B端进入电场L/8时的加速度大小和方向;
⑵棒在运动过程中的最大动能;
⑶棒的最大电势能。(设O点处电势为零)
参考答案:⑴a=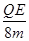 ,方向水平向右;⑵Ekm=
,方向水平向右;⑵Ekm=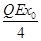 +
+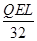 ;⑶若x0=L,Epm=
;⑶若x0=L,Epm= ,若x0<L,Epm=
,若x0<L,Epm=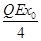 +
+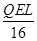 +
+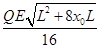 ,若x0>L,Epm=
,若x0>L,Epm=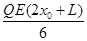
本题解析:⑴当棒的B端进入电场L/8时,对绝缘棒受重力mg、水平面的支持力N、水平向右的恒力QE/4和水平向左的电场力qE作用,根据牛顿第二定律有:QE/4-qE=ma?①
由于棒绝缘,且电荷分布均匀,所以有:q=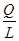 ×
×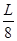 ?②
?②
由①②式联立解得:a=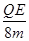 ,方向水平向右
,方向水平向右
⑵开始时,棒在水平向右恒力作用下向右做匀加速直线运动,棒开始进入电场时,受到了水平向左的电场力作用,且电场力的大小随棒进入电场中长度的增大而增大,将先做加速度逐渐减小的加速运动,当加速度减小到0时,棒的速度达到最大,即动能最大,设此时棒进入电场中的长度为x,有: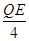 =
=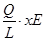 ③
③
根据动能定理有: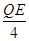 (x0+x)-
(x0+x)-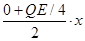 =Ekm-0?④
=Ekm-0?④
由③④式联立解得:Ekm=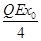 +
+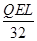
⑶随着棒进入电场中长度的继续增大,棒将要做减速运动,当棒速度减为0时,棒的电势能最大
若x0=L,棒恰好全部进入电场,根据动能定理有: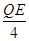 (x0+L)-
(x0+L)-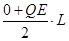 =0-0
=0-0
棒的电势能为:Epm=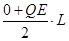 =
=
若x0<L,棒一部分进入电场,设进入的长度为l,根据动能定理有: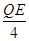 (x0+l)-
(x0+l)-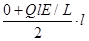 =0-0
=0-0
解得:l=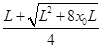 ,棒的电势能为:Epm=
,棒的电势能为:Epm=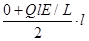 =
=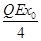 +
+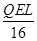 +
+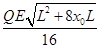
若x0>L,棒全部进入电场,且A端离O点距离为l,有: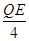 (x0+l)-
(x0+l)-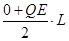 -QE(l-L)=0-0
-QE(l-L)=0-0
解得:l=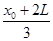 ,棒的电势能为:Epm=
,棒的电势能为:Epm=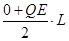 +QE(l-L)=
+QE(l-L)=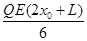
本题难度:一般
3、计算题 如图甲所示,足够长的固定光滑细杆与地面成一定倾角,在杆上套有一个光滑小环,沿杆方向给环施加一个拉力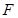 ,使环由静止开始自底端沿杆向上运动,已知拉力
,使环由静止开始自底端沿杆向上运动,已知拉力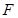 及小环速度
及小环速度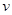 随时间
随时间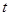 变化的规律如图乙所示(重力加速度
变化的规律如图乙所示(重力加速度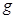 取10 m/s2)。
取10 m/s2)。
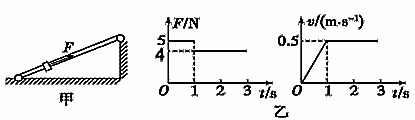
(1)求小环的质量大小
(2)若在1.5s末撤除力F,则撤除力F后物体经多长时间回到细杆底端
参考答案:(1)2kg?(2)1s
本题解析:(1)分析小环受力:重力mg,沿杆子拉力F,杆子的弹力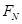 ,
,
设杆子与水平方向倾角为θ,在0~1s内有F=5N,小环匀加速运动,

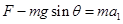
1s后F=4N,小环匀速运动,有
由图像知,0~1s内加速度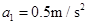
解得m=2kg
(2) 0~1s内小环向上匀加速运动的位移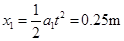
在1~1.5s内匀速运动的位移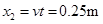
撤除力F后,小环运动加速度大小为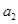 ,且
,且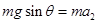 ,解得
,解得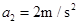
撤除力F后小环继续向上减速运动,初速度v=0.5m/s,到达最高点的时间
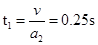 )
)
 时间内位移
时间内位移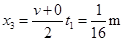
到达最高点后,小环向下加速运动,设小环由最高点到底端时间为t2
有: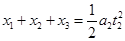
解得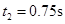
撤除力F后小环运动到杆子底端总时间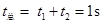
点评:中等难度。多过程问题可以把每个小过程分开研究,把一个大题拆成多个小题研究可以使问题简化。
本题难度:简单
4、选择题 如图所示,两车厢的质量相同,其中一个车厢内有一人拉动绳子使两车厢相互靠近。若不计绳子质量及车厢与轨道间的摩擦,下列对于哪个车厢里有人的判断正确的是
[? ]
A.绳子的拉力较大的那一端车厢里有人?
B.先开始运动的车厢里有人
C.后到达两车中点的车厢里有人
D.不去称量质量无法确定哪个车厢有人
参考答案:C
本题解析:
本题难度:一般
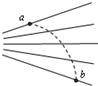
5、选择题 如图所示,实线是电场中一簇方向未知的电场线,虚线是一个带电粒子从a点运动到b点的轨迹,若带电粒子只受电场力作用,粒子从a点运动到b点的过程中( )
A.带电粒子一定带负电
B.运动的加速度逐渐增大
C.运动的速度逐渐减小
D.粒子的电势能逐渐减小