1、选择题 甲、乙两个物体的质量分别为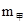 和
和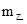 ,并且
,并且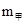 =2
=2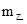 ,它们与水平桌面的动摩擦因数相同,当它们以相同的初动能在桌面上滑动时,它们滑行的最大距离之比为(?).
,它们与水平桌面的动摩擦因数相同,当它们以相同的初动能在桌面上滑动时,它们滑行的最大距离之比为(?).
A.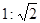
B.2:1
C.1:1
D.1:2
参考答案:D
本题解析:由动能定理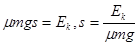 ,它们滑行的最大距离之比为1:2,故选D
,它们滑行的最大距离之比为1:2,故选D
点评:难度较小,处理此类问题首先要分析受力和做功情况
本题难度:一般
2、简答题

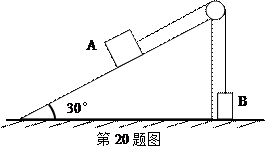
求:(1) B的速度是多少?
(2)此过程中线的拉力对B做功是多少?
参考答案:
(1)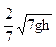 ?(2)
?(2)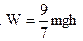
本题解析:(1)B上升高度h时,A沿斜面下滑距离h,下滑高度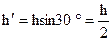
以A、B整体为研究对象,由机械能守恒得:
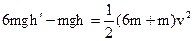 ?
?
(2)对B由动能定理得:?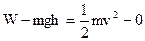
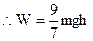
本题难度:简单
3、选择题 物体在水平恒力作用下,在水平面上由静止开始运动.当位移s时撤去F,物体继续前进3s后停止运动,若路面情况相同,则物体的摩擦力和最大动能是( )
A.f=
,Ek=4Fs
B.f=,Ek=Fs
C.f=,Ek=
D.f=,Ek=
参考答案:在物体的整个运动过程中,由动能定理得:
Fs-f(s+3s)=0-0
解得:f=F4;
从物体开始运动到撤去外力的过程中,由动能定理得:
Fs-fs=Ekm-0
解得:Ekm=3Fs4;所以选项D正确,ABC错误.
故选:D.
本题解析:
本题难度:一般
4、简答题
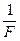
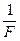
(1)在提升重物的过程中,除了重物的质量和所受重力保持不变以外,在第一个时间段内和第二个时间段内还各有一些物理量的值保持不变。请分别指出第一个时间段内和第二个时间段内所有其他保持不变的物理量,并求出它们的大小;
(2)求被提升重物在第一个时间段内和第二个时间段内通过的总路程。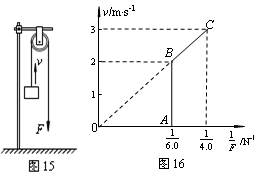
参考答案:(1) ?(2) 2.75m
?(2) 2.75m
本题解析:(1)由v-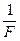 图象可知,第一时间段内重物所受拉力保持不变,且F1=6.0N…1分
图象可知,第一时间段内重物所受拉力保持不变,且F1=6.0N…1分
因第一时间段内重物所受拉力保持不变,所以其加速度也保持不变,设其大小为a,
根据牛顿第二定律有F1-G=ma,…………………………………………………2分
重物速度达到vC=3.0m/s时,受平衡力,即G=F2=4.0N,
由此解得重物的质量 ?…………………………………………………2分
?…………………………………………………2分
联立解得? a =5.0m/s2 …………………………………………………………………1分
在第二段时间内,拉力的功率保持不变 ………………………………2分
………………………………2分
(2)设第一段时间为t1,重物在这段时间内的位移为x1,则
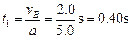 ,
,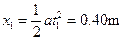 ………………………………………2分
………………………………………2分
设第二段时间为t2,t2=t-t1=1.0s…………………………………………………1分
重物在t2这段时间内的位移为x2,根据动能定理有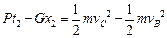 …3分
…3分
解得?x2="2.75m" …………………………………………………………………………1分
本题难度:一般
5、计算题 为了研究过山车的原理,某兴趣小组提出了下列设想:取一个与水平方向夹角为37°、长为l=2.0m的粗糙倾斜轨道AB,通过水平轨道BC与竖直圆轨道相连,出口为水平轨道DE,整个轨道除AB段以外都是光滑的。其AB与BC轨道以微小圆弧相接,如图所示。一个小物块以初速度v0=4.0m/s从某一高处水平抛出,到A点时速度方向恰好沿AB方向,并沿倾斜轨道滑下。已知物块与倾斜轨道的动摩擦因数μ=0.50。(g=10m/s2、sin37°=0.60、cos37°=0.80)
(1)求小物块到达A点时速度。
(2)要使小物块不离开轨道,并从轨道DE滑出,求竖直圆弧轨道的半径应该满足什么条件?
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则竖直圆轨道的半径应该满足什么条件?

参考答案:解:(1)小物块做平抛运动,经时间t到达A处时,令下落的高度为h,水平分速度v0,竖直速度为vy,小物块恰好沿斜面AB方向滑下,则tan37°=vy/v0
得vy=3 m/s,所以小物块到A点的速度为5m/s
(2)物体落在斜面上后,受到斜面的摩擦力Ff=μFN=μmgcos37°
设物块进入圆轨道到达最高点时有最小速度v1,此时物块受到的重力恰好提供向心力,令此时的半径为 R0,则mg=mv12/R0
物块从抛出到圆轨道最高点的过程中,根据动能定理有:
mg(h+lsin37°-2R0)-μmgcos37°·l = mv12/2-mv02/2
联立上式,解得R0=0.66m
若物块从水平轨道DE滑出,圆弧轨道的半径满足R1≤0.66m
(3)为了让小物块不离开轨道,并且能够滑回倾斜轨道AB,则物块上升的高度须小于或于某个值R,则mg(h+lsin37°)/μmgcos37°·l-mgR=0-mv02/2
解得R=1.65m
物块能够滑回倾斜轨道AB,则R2≥1.65m
本题解析:
本题难度:困难