1、计算题  （10分）如下图所示，光滑水平桌面上有长L＝2 m的挡板C，质量mC＝5 kg，在其正中央并排放着两个小滑块A和B，mA＝1 kg，mB＝3 kg，开始时三个物体都静止。在A、B间放有少量塑胶炸药，爆炸后A以6 m/s速度水平向左运动，A、B中任意一块与挡板C碰撞后，都粘在一起，不计摩擦和碰撞时间，求：

①当两滑块A、B都与挡板C碰撞后，C的速度是多大？
②A、C碰撞过程中损失的机械能。

参考答案：（1）（2）15J

本题解析：① A、B、C系统动量守恒
解得：.
②炸药爆炸时A、B系统动量守恒
解得：　所以A、C先碰
A、C碰撞前后系统动量守恒

故

本题难度：一般

2、简答题  如图所示，在高为0.8m的光滑桌面上放着一个质量为1.99kg的木块，一颗质量为10g的铅弹，以某一速度从水平方向射中木块，并把木块打落在地面上，落地点与桌面的水平距离为0.4m．铅弹射中木块后留在木块中，设增加的内能有50%使铅弹的温度升高，则铅弹的温度升高多少摄氏度？已知铅的比热容为1.3×102J/（kg-℃），取g=10m/s2．

参考答案：设铅弹初速度为v0，击中木块后的共同速度为v，离开桌面到落地用时t，打击过程中产生的总内能为Q，则
根据平抛运动的规律得
h=12gt2
s=vt
解得?v=1m/s?
由系统动量守恒得mv0=（m+M）v
?得v0=200m/s
根据能量守恒得?
12mv20=12(m+M)v2+Q
50%Q=cm△t
得△t=76.6℃
答：铅弹的温度升高76.6℃．

本题解析：

本题难度：一般

3、简答题  相隔一定距离的A、B两球，质量相等，假定它们之间存在着恒定的斥力作用．原来两球被按住，处在静止状态．现突然松开，同时给A球以初速度v0，使之沿两球连线射向B球，B球初速度为零．若两球间的距离从最小值（两球未接触）到刚恢复到原始值所经历的时间为t0，求B球在斥力作用下的加速度．

参考答案：以m表示每个球的质量，F表示恒定的斥力，l表示两球间的原始距离，松手后，A球做初速度为v0的匀减速直线运动，B球做初速度为零的匀加速直线运动．设在两球间的距离由l减小恢复到l的过程中，A球的路程为l1，B球的路程为l2，刚恢复到原始长度时，A球的速度为v1，B球的速度为v2．由动量守恒定律有：
mv0=mv1+mv2
由功能关系得，Fl1=12mv02-12mv12
Fl2=12mv22
由于初状态和末状态两球之间的距离相等，故有l1=l2
由以上解得v2=v0
当两球速度相等时，距离最小，设此时球的速度为u，则由动量守恒得，
mv0=（m=m）u
设B的加速度为a，有v2=u+at0
解得a=v02t0．
答：B球在斥力作用下的加速度为a=v02t0．

本题解析：

本题难度：一般

4、计算题  如图14所示，两个完全相同的质量为m的木板A、B置于水平地面上，它们的间距s="2.88m." 质量为2m、大小可忽略的物块C置于A板的左端。C与A之间的动摩擦因数为?μ1=0.22,A、B与水平地面之间的动摩擦因数为μ2=0.10，最大静摩擦力可认为等于滑动摩擦力。开始时，三个物体处于静止状态，现给C施加一个水平向右，大小为的恒力F，假定木板A、B碰撞时间极短且碰撞后粘连在一起。要使C最终不脱离木板，每块木板的长度至少应为多少？

参考答案：0.3 m

本题解析：略

本题难度：简单

5、简答题  质量分别为3m和m的两个物体，用一根细线相连，中间夹着一个被压缩的轻质弹簧，整个系统原来在光滑水平地面上以速度V0向右匀速运动，如图所示。后来细线断裂，质量为m的物体离开弹簧时的速度变为2V0。求
（1）质量为3m的物体最终的速度；
（2）绳断前弹簧的弹性势能。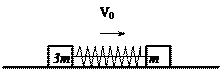

参考答案：
（1）（2）

本题解析：设3m的物体离开弹簧时的速度为，由动量守恒定律得：
?(4分)?
所以??(3分)
由能量守恒定律得：?(4分)
所以弹性势能??(3分)

本题难度：简单