1、计算题  渔船常利用超声波来探测远处鱼群的方位。已知某超声波频率为1.0×105 Hz，某时刻该超声波在水中传播的波动图象如图所示。
（1）从该时刻开始计时，画出x=7.5×10-3 m处质点做简谐运动的振动图象（至少一个周期）；
（2）现测得超声波信号从渔船到鱼群往返一次所用时间为4s，求鱼群与渔船间的距离（忽略船和鱼群的运动）。

参考答案：解：（1）该波的周期为，由波动图象知，此时x=7.5×10-3 m处的质点位于负的最大位移处，所以，从该时刻开始计时，该质点的振动图像，如图所示

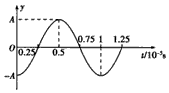
（2）由波形图读出波长λ=15×10-3 m
由波速公式得v=λf
鱼群与渔船的距离为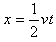
联立以上两式，代入数据得x=3 000 m

本题解析：

本题难度：一般

2、选择题 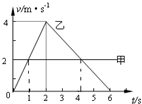 甲、乙两物体由同一位置出发沿一直线运动，其v-t图象如右图所示．下列说法正确的是
A.2s后，甲、乙两物体的速度方向相反
B.甲做匀速直线运动，乙做匀变速直线运动
C.两物体两次速度相等的时刻分别是在1s末和4s末
D.乙在前2s内做匀加速直线运动，2s后做匀减速直线运动

参考答案：CD

本题解析：分析：由图两物体速度始终为正值，速度方向一直为正方向，相同．甲做匀速直线运动，而乙的加速度是变化的，不是匀变速直线运动．由图读出速度相同的两个时刻．乙在前2s内做匀加速直线运动，2s后做匀减速直线运动．
解答：A、由图可知两物体的速度方向一直为正方向，相同．故A错误．
? B、甲做匀速直线运动，而乙的加速度方向先正后负，加速度是变化的，不是匀变速直线运动．故B错误．
? C、由图：纵坐标表示速度，速度相同的两个时刻分别为在1s末和4s末．故C正确．
? D、乙在前2s内速度均匀增大，做匀加速直线运动，2s后速度均匀减小，做匀减速直线运动．故D正确．
故选CD
点评：本题考查对速度图象的理解能力．对于匀变速直线运动，速度图象是斜率的直线，加速度应恒定不变．

本题难度：一般

3、填空题  如图所示，质点沿直线做简谐运动，平衡位置在O点，某时刻通过P点向右运动，经1s再次回到P点，再经1s到达O点，若OP=2cm，则质点运动的周期T=______s，质点运动的振幅为A=______cm．

参考答案：从P点向最大位移处运动，又回到P点，用时为1s，根据简谐运动的对称性，知P点到最大位移处运行的时间为0.5s，则T4=1+0.5s=1.5s，所以T=6s．
从平衡位置开始，经过T6运动到x=2cm处，则x=Asinωt=Asinπ3，解得A=43

本题解析：

本题难度：一般

4、计算题  一列简谐波在均匀介质中传播，从波源的振动传播到b点时开始计时，图甲所示为t＝0.25 s时刻介质中的波动图象，图乙为b点从t＝0 s开始计时的振动图象，

求：(1)这列简谐波的传播方向；
(2)t1＝0.25 s时刻，质点O的速度方向；
(3)质点做简谐运动的频率;
(4)简谐波传播速度的大小．

参考答案：(1) 向x轴负方向传(2) y轴正方向(3) (3) 2 Hz? (4) 8 m/s.

本题解析：(1)由题图乙，b点在0.25 s时速度方向向下，故波向x轴负方向传播------(1分)
(2)O点：y轴正方向? ------------（1分）
(3)由题图乙知T＝0.5 s? ------------（1分）
故? f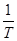＝＝2 Hz? ------------（1分）
(4)由题图甲知λ＝4 m.? ------------（1分）
故v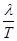＝＝8 m/s.?------------（1分）
本题考查机械波的波动图像和振动图像，根据前代后后跟前可判断波的传播方向，由振动图像可直接读出周期，波动图像中可直接读出波长，由公式v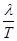＝可求出波速

本题难度：简单

5、填空题  如图所示，一个光滑水平面上做简谐运动的弹簧振子，滑块A的质量为M、弹簧的劲度系数为k．现在振子上面放另一个质量为m的小物体B，它与振子一起做简谐运动，则小物体B受到的恢复力f跟位移x的关系式是______．（位移是指相对于振子平衡位置的位移）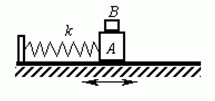

参考答案：整体做简谐运动，则对整体有：f′=-kx；
则整体的加速度a=-kxM+m
对于m由牛顿第二定律可知：
f=ma=-mM+mkx；
故答案为：f=-mM+mkx

本题解析：

本题难度：一般