1、计算题 串列加速器是用来产生高能离子的装置。图中虚线框内为其主体的原理示意图,其中加速管的中部b处有很高的正电势U,a、c两端均有电极接地(电势为零)。现将速度很低的负一价碳离子从a端输入,当离子到达b处时,可被设在b处的特殊装置将其电子剥离,成为n价正离子,而不改变其速度大小。这些正n价碳离子从c端飞出后进入一与其速度方向垂直的、磁感应强度为B的匀强磁场中,在磁场中做半径为R的圆周运动。已知碳离子的质量为m=2.0×10-26 kg,U=7.5×105V,B=0.50T,n=2,元电荷e=1.6×10-19 C,求R。
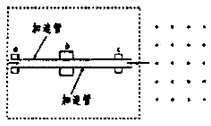
参考答案:解:设碳离子到达b处的速度为v1,从c端射出时的速度为v2,由能量关系得
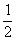 m
m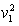 =eU ①
=eU ①
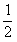 m
m =
=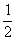 m
m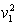 +neU ②
+neU ②
进入磁场后,碳离子做圆周运动,可得nev2B=m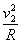 ③
③
由以上三式可得R=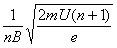 ④
④
由④式及题给数值得R=0.75m
本题解析:
本题难度:一般
2、计算题 电子所带电荷量最早是由美国科学家密立根所做的油滴实验测得的。密立根油滴实验的原理如图所示:两块水平放置的平行金属板与电源相连接,上板带正电,下板带负电,油滴从喷雾器喷出后,由于与喷嘴摩擦而带负电,油滴散布在油滴室中,在重力作用下,少数油滴通过上面金属板的小孔进入(可认为初速度为0)平行金属板间,落到两板之间的匀强电场中。在强光照射下,观察者通过显微镜观察油滴的运动。
从喷雾喷出的小油滴可以视为球形,小油滴在空气中下落时受到的空气阻力f大小跟它下落的速度v的大小的关系是:f=6πηrv,式中r为油滴半径,η为粘滞系数。设重力加速度为g,不考虑油滴的蒸发。

(1)实验中先将开关断开,测出小油滴下落一段时间后达到匀速运动时的速度v1,已知油的密度为ρ,空气的密度为ρ′,粘滞系数为η,试由以上数据计算小油滴的半径r;
(2)待小球向下运动的速度达到v1后,将开关闭合,小油滴受电场力作用,最终达到向上匀速运动,测得匀速运动的速度v2,已知两金属板间的距离为d,电压为U。试由以上数据计算小油滴所带的电荷量q;
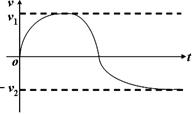
(3)大致(不要求精确的标度)画出油滴从进入平行金属板到向上匀速运动这段过程中的v—t图像(设竖直向下为正方向)。
参考答案:(1) ?(2)
?(2)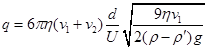
(3)
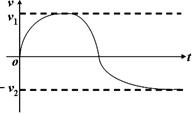
本题解析:(1)小油滴向下匀速运动,重力和空气阻力、空气浮力达到平衡
有: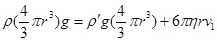 (4分)
(4分)
得: (2分)
(2分)
(2)小油滴在电场中向上匀速运动,重力、空气阻力和电场力、空气浮力达到平衡
有: ?(4分)
?(4分)
得: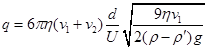 ?(2分)
?(2分)
(3)小油滴先在重力、浮力、空气阻力的作用下向下做加速度减小的加速运动;闭合开关后有了向上的电场力,接着向下做加速度增大的减速直到速度较小为零,然后向上做加速度减小的加速运动,最后向上匀速。如右图所示:(4分:图线形状<含方向>2分、速度临界线2分)
本题难度:一般
3、计算题 (15分)如图所示,极板A、B、K、P连入电路,极板P、K,A、B之间分别形成电场,已知电源电动势E=300V,电源内阻不计 ,电阻R1="2000KΩ," R2=1000KΩ,A、B两极板长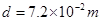 ,间距
,间距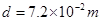 。一个静止的带电粒子,电荷量
。一个静止的带电粒子,电荷量 、质量
、质量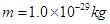 ,从极板K中心经 P、K间电场加速后,进入极板A、B间电场中发生偏转。(极板间电场可视为匀强电场且不考虑极板边缘效应,不计粒子重力)求:
,从极板K中心经 P、K间电场加速后,进入极板A、B间电场中发生偏转。(极板间电场可视为匀强电场且不考虑极板边缘效应,不计粒子重力)求:
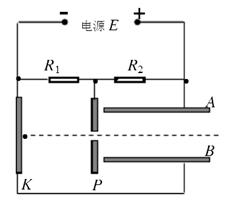
⑴极板P、K之间电压UPK,A、B之间电压UAB
⑵粒子刚进入偏转极板A、B时速度v0
⑶粒子通过极板A、B时发生偏转距离y
参考答案:(1)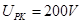
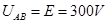 (2)
(2) (3)
(3)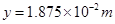
本题解析: (1)极板PK之间的电压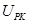 即为
即为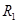 两端电压,所以
两端电压,所以
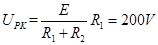 ?3分
?3分
AB之间的电压为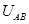 ,所以
,所以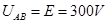 ? 3分
? 3分
(2)由动能定理可得: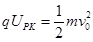 ,解得
,解得 ,代入数据可得:
,代入数据可得:
(3)粒子在极板AB之间轨迹为抛物线,测移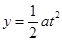 ?2分
?2分
而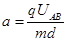 ,
,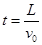 ,所以
,所以 ,代入数据可得:
,代入数据可得: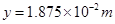
本题难度:一般
4、简答题 如图所示,A、B为真空中相距为d的一对平行金属板,两板间的电压为U,一带电粒子从A板的小孔进入电场,粒子的初速度可视为零,经电场加速后从B板小孔射出。已知带电粒子的质量为m,所带电荷量为q。带电粒子所受重力不计。求:
(1)带电粒子从B板射出时的速度大小;
(2)带电粒子在电场中运动的时间。
参考答案:(1)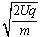 (2)
(2)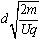
本题解析:(1)设带电粒子从B板射出时的速度为v,根据动能定理:

(2)以带电粒子为研究对象,设带电粒子在电场中运动的时间为t,根据运动学公式
设带电粒子在电场中的加速度为a,
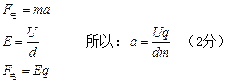 ?
?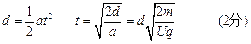
本题难度:简单
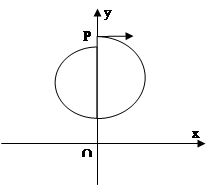
5、计算题 (22分)如图所示,在xoy平面内第二象限的某区域存在一个圆形匀强磁场区,磁场方向垂直xoy平面向外。一电荷量为e、质量为m的电子,从坐标原点O处以速度v0射入第二象限,速度方向与y轴正方向成30°角,经过磁场偏转后,通过P(0,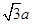 )点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为
)点,速度方向垂直于y轴,不计电子的重力。电子在圆形磁场区域中作圆周运动的轨道半径为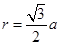 ,求:
,求:

(1)电子从坐标原点O 运动到P点的时间t1;
(2)所加圆形匀强磁场区域的最小面积;
(3)若电子到达y轴上P点时,撤去圆形匀强磁场,同时在y轴右侧加方向垂直xoy平面向里的匀强磁场,磁感应强度大小为B1,在y轴左侧加方向垂直xoy平面向里的匀强磁场,电子在第(k+1)次从左向右经过y轴(经过P点为第1次)时恰好通过坐标原点。求y轴左侧磁场磁感应强度大小B2及从P点运动到坐标原点的时间t2
参考答案:(1)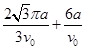 (2)
(2) (3)
(3)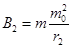 ?
?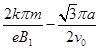
本题解析:(1)由几何关系,电子从O点运动到P点的路程为:
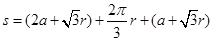
将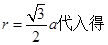
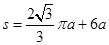
所以从O点运动到P点的时间为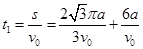
(2)以AB为直径的圆形磁场即为最小的圆形磁场区域,最小面积为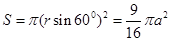
(3)设电子在y轴右侧和左侧做圆周运动的半径分别为r1和r2,则有

如图乙的几何关系可知
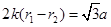
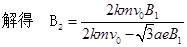
设电子在y轴右侧和左侧做圆周运动的周期分别为T1和T2, 则
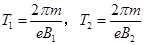
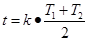
解得 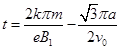
本题考查的是带电粒子在磁场中的运动问题,根据几何关系,应用带电粒子在磁场中的运动的相关公式,即可计算出结果;
本题难度:一般
Friends are thieves of time. 朋友是时间的浪费者. / 浪费朋友的时间,就是谋财害命.