1、填空题  在竖直平面内，一根光滑金属杆弯成如图所示形状，相应的曲线方程为y＝2.5 cos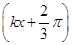（单位：m），式中k＝1m－1。将一光滑小环套在该金属杆上，并从x＝0处以v0＝5m/s的初速度沿杆向下运动，取重力加速度g＝10m/s2。则当小环运动到x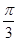＝m时的速度大小v＝__________m/s；该小环在x轴方向最远能运动到x＝__________m处。

参考答案：，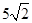

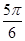
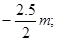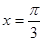本题解析：光滑小环在沿金属杆运动的过程中，只有重力做功，机械能守恒，由曲线方程可知，环在x=0处的y坐标是在时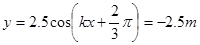，，选y=0处为零势能参考平面，则有，解得
当环运动到最高点时，速度为零，同理有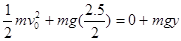，解得y=0，即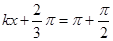，该小环在x轴方向最远能运动到处
点评：本题难度较大，换在运动过程中，机械能守恒，根据曲线方程可以确定环的位置

本题难度：一般

2、选择题  如图所示，一物体以初速度v0冲向光滑斜面AB，并能沿斜面升高h.下列说法中正确的是（?）

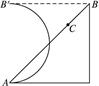
A．若把斜面从C点锯断，由机械能守恒定律知，物体冲出C点后仍能升高h
B．若把斜面弯成圆弧形，物体仍能沿AB′升高h
C．若把斜面从C点锯断或弯成圆弧状，物体都不能升高h，因为机械能不守恒
D．若把斜面从C点锯断或弯成圆弧状，物体都不能升高h，但机械能仍守恒

参考答案：D

本题解析：物体到达B时速度为零,由机械能守恒定律有mgh=mv02.若从C锯断,到达最高点时物体有水平速度,则mgh′+mvx2=mv02,h′<h;若把斜面弯成圆弧状,到达圆弧最高点时速度v<,则不能到达最高点B′处,答案为D.

本题难度：简单

3、计算题  如图所示，两平行金属板A、B水平放置，两板间的距离d=40cm．电源电动势E=24V，内电阻r=1Ω，电阻R=15Ω．闭合开关S，待电路稳定后，在两板之间形成匀强电场．在A板上有一个小孔k，一个带电荷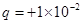量为C、质量为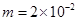kg的粒子P由A板上方高h=10cm处的O点自由下落，从k孔进入电场并打在B板上点处．当P粒子进入电场时，另一个与P相同的粒子Q恰好从两板正中央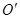点水平飞入．那么，滑动变阻器接入电路的阻值为多大时，粒子Q与P恰好同时打在处。 （粒子间的作用力及空气阻力均忽略不计，取g=10m/s2）

参考答案：滑动变阻器接入电路的阻值为8Ω

本题解析：
试题分析:根据机械能守恒定律可得P粒子进入电场时的速度为：
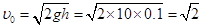m/s
设P、Q在电场中运动的加速度为a，运动到打在点的时间为t，则：
对P：?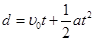
对Q：
联立解得：s，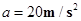
而
所以，滑动变阻器两端的电压为：

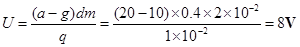
由欧姆定律可得通过滑动变阻器的电流为：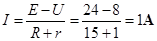
所以，滑动变阻器接入电路的阻值为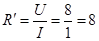：Ω

本题难度：一般

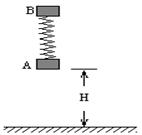
4、简答题  如图所示，质量均为m的物块A和B用弹簧连结起来，将它们悬于空中静止，弹簧处于原长状态，A距地面高度H=0.90m，同时释放两物块，A与地面碰撞后速度立即变为零，由于B的反弹，A刚好能离开地面。若B物块换为质量为2m的物块C（图中未画出），仍将它们悬于空中静止且弹簧为原长，从A距地面高度为H’处同时释放，设A也刚好能离开地面。已知弹簧的弹性势能EP与弹簧的劲度系数k和形变量x的关系是：EP=kx2。试求：（1）B反弹后，弹簧的最大伸长量。（2）H’的大小

参考答案：（1）0.6m?（2）0.75m

本题解析：（1）A落地时，B的速度为
υB=?①
设反弹后上升的最大高度为x，
A恰好离开地面时 kx="mg?" ②
由系统机械能守恒?mυB2=mgx+kx2?③
由①②③联立得? x="0.6m"
（2）将B换成C后，A落地时，C的速度为? υC=?
C反弹后上升到最高时A刚好离开地面，?故仍有 kx=mg
由系统机械能守恒
·2mυc2=2mgx+kx2?解得：H’=0.75m

本题难度：一般

5、计算题  如图所示，一个质量为0.6kg的小球以某一初速度从P点水平抛出，恰好从光滑圆弧AB的A点的切线方向进入圆弧(不计空气阻力，进入圆弧时无机械能损失)，并从最低点B通过一段光滑小圆弧滑上另一粗糙斜面CD。已知圆弧AB的半径R=0.9m,θ=600,B在O点正下方，斜面足够长，动摩擦因数u=0.5，斜面倾角为370，小球从p到达A点时的速度为4m/s。（g取10m/s2，cos37°=0.8，sin37°=0.6）问：

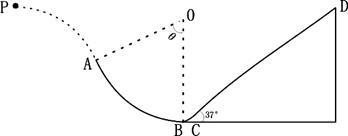
（1）P点与A点的水平距离和竖直高度
（2）小球在斜面上滑行的总路程

参考答案：(1) x=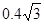m；y=0.6m；（2）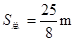

本题解析：
试题分析: （1）A点的水平分速度为：vAx= vAcos60°=2m/s，
竖直分速度为：vAy= vAsin60°=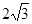m/s，时间t= vAy/g=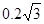s
P点与A点的水平距离x= vAxt=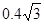m
P点与A点的竖直高度y==0.6m
（2）设小球斜面向上运动的距离为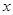，则

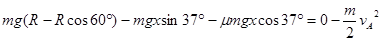
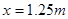?再滑下时设过了A点，则


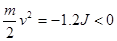
故小球不能过A点，只能来回摆动，最后停在B点，由能量守恒定律

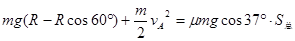
得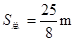：?（1分）

本题难度：一般