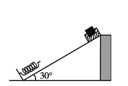
1、选择题  如图为某探究活动小组设计的节能运输系统．斜面轨道倾角为30°，质量为M的木箱与轨道的动摩擦因数为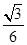.木箱在轨道顶端时，自动装货装置将质量为m的货物装入木箱，然后木箱载着货物沿轨道无初速度滑下，当轻弹簧被压缩至最短时，自动卸货装置立刻将货物卸下，然后木箱恰好被弹回到轨道顶端，再重复上述过程．下列选项正确的是(　　)

A．m＝M
B．m＝2M
C．木箱不与弹簧接触时，上滑的加速度大于下滑的加速度
D．在木箱与货物从顶端滑到最低点的过程中，减少的重力势能全部转化为弹簧的弹性势能

参考答案：：BC

本题解析：：木箱和货物下滑过程中，令下滑高度为h，根据功能关系有(M＋m)gh－μ(M＋m)gh＝E弹．
木箱上滑过程中，根据功能关系有－Mgh－μMgh＝0－E弹．代入相关数据，整理得m＝2M，A错误，B正确；木箱和货物下滑过程中，根据牛顿第二定律有： a1＝g(sin θ－μcos θ)，方向沿斜面向下．
木箱上滑过程中，根据牛顿第二定律有： a2＝g(sin θ＋μcos θ)，方向沿斜面向下，所以C正确；
根据能量守恒定律知，还有一部分机械能由于克服摩擦力做功转化为内能，D错误．

本题难度：简单

2、计算题  （18分）如图所示，圆管构成的半圆形轨道竖直固定在水平地面上，轨道半径为R，MN为直径且与水平面垂直，直径略小于圆管内径的小球A以某一速度冲进轨道，到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞，碰后两球粘在一起飞出轨道，落地点距N为2 R。重力加速度为g，忽略圆管内径，空气阻力及各处摩擦均不计，求

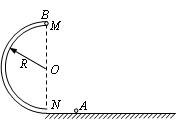
（1）粘合后的两球从飞出轨道到落地的时间t；
（2）小球A冲进轨道时速度v的大小。
（3）小球A与小球B球碰撞前瞬间对轨道的压力多大？方向如何？

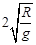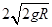参考答案：（1）?（2）?（3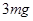）?，?方向竖直向上

本题解析：（1）粘合后的两球飞出轨道后做平抛运动，竖直方向分运动为自由落体运动，有
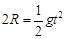?①? ( 2分)?
解得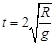②? (1分)
（2）设球A的质量为m，碰撞前速度大小为v1，把球A冲进轨道最低点时的重力势能定为0，
由机械能守恒定律知 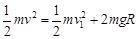?③(3分)
设碰撞后粘合在一起的两球速度大小为v2，
由动量守恒定律知 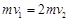?④( 3分)
飞出轨道后做平抛运动，，有 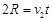?⑤ (2分 )
综合②③④⑤式得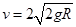?(2分 )
(3)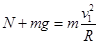? (2分 )
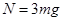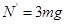? (1分)
?(1分)
方向竖直向上(1分)

本题难度：一般

3、计算题  质量分别为m1和m2的两个小球叠放在一起，从高度为h处自由落下，如图所示。已知h远大于两球半径，所有的碰撞都是完全弹性碰撞，且都发生在竖直方向上。若碰撞后m2恰处于平衡状态，求

（i）两个小球的质量之比m1:m2；
（ii）小球m1上升的最大高度。

参考答案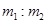：=1:3；H=4h

本题解析：下降过程为自由落体运动，触地时两球速度相同，V=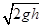,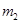碰撞地之后，速度瞬间反向，大小相等，选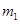与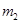碰撞过程为研究过程，碰撞前后动量守恒，设碰后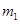速度大小分别为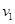，碰后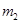处于平衡状态，速度为0
选向上方向为正方向，则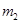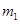：（-）V=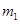
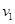
由能量守恒定律得：（+）=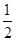
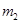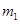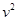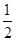
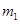
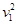
联立解得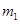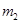：:=1:3
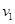=2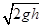
反弹后高度为：H=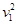/(2g)=4h

本题难度：一般

4、选择题  如图所示，半径r=0.5m的光滑圆轨道被竖直固定在水平地面上，圆轨道最低处有一小球（小球的半径比r小很多）。现给小球一个水平向右的初速度v0，要使小球不脱离轨道运动，v0应满足

[? ]
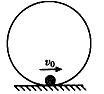
A.
B.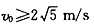
C.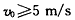
D.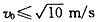

参考答案：CD

本题解析：

本题难度：一般

5、选择题  下列情形中物体机械能守恒的是（　　）
A．物体在某恒力的作用下沿水平方向做加速运动
B．自由落体运动
C．匀速降落的跳伞运动员
D．飞机在跑道上加速滑行准备起飞

参考答案：A、物体在某恒力的作用下沿水平方向做加速运动，动能增加，势能不变，故机械能增加，故A错误；
B、自由落体运动总有重力做功，机械能守恒，故B正确；
C、匀速降落的跳伞运动员，势能减小，动能不变，故机械能减小，故C错误；
D、飞机在跑道上加速滑行准备起飞，动能增加，势能不变，故机械能增加，故D错误；
故选B．

本题解析：

本题难度：简单