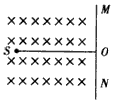
1、计算题  S为电子源，它只在下图所示的纸面上360°范围内发射速率相同、质量为m、电荷量为e的电子，MN是一块足够大的竖直挡板，与S的水平距离OS=L。挡板左侧有垂直纸面向里的匀强磁场，磁感应强度为B，求：
(1)要使S发射的电子能够到达挡板，则发射电子的速度至少为多大？
(2)若电子发射的速度为eBL/m，则挡板被击中的范围有多大？

2、选择题  如图所示，带正电的物块A放在足够长的不带电小车B上，两者均保持静止，处在垂直纸面向里的匀强磁场中，在t=0时用水平恒力F向右拉小车B，t=t1时A相对B开始滑动，已知地面光滑、AB间粗糙，A带电荷量保持不变，则关于A、B的v-t图象，下图大致正确的是

[? ]
A．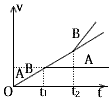
B．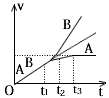
C．
D．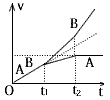

3、计算题  如图所示，在平面直角坐标系的第二和第三象限区域内有沿y轴负方向的匀强电场，第四象限内存在一水平方向的半径r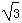＝m的圆形匀强磁场，圆心O′坐标为(2，－6)，磁感应强度B＝0.02 T，磁场方向垂直坐标轴向里。坐标(－2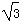，)处有一粒子发射源，水平发射一质量m＝2.0×10-11 kg、带电荷量q＝1.0×10-5 C的正电荷，初速度为v0＝1.0×104 m/s，粒子从O点射入第四象限，且在O点时速度方向指向O′，不计粒子的重力。求：
(1)电场强度的大小；
(2)带电粒子再次经过x轴的位置；
(3)带电粒子在第四象限运动的时间。

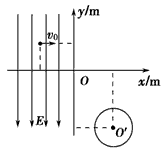
4、计算题  如下图，在xOy坐标系的第一象限内有互相正交的匀强电场E与匀强磁场B，E的大小为1.0×103V/m，方向未知，B的大小为1.0T，方向垂直纸面向里；第二象限的某个圆形区域内，有方向垂直纸面向里的匀强磁场B′。一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与x轴负方向60°角从A点沿直线进入第一象限运动，经B点即进入处于第二象限内的磁场B′区域，一段时间后，微粒经过x轴上的C点并与x轴负方向成60°角的方向飞出。已知A点的坐标为（10，0），C点的坐标为（-30，0），不计粒子重力，g取10m/s2。
小题1:请分析判断匀强电场E的方向并求出微粒的运动速度v；
小题2:匀强磁场B′的大小为多大？
小题3:B′磁场区域的最小面积为多少？

5、计算题  如图，在0≤x≤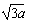区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B。在t＝0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内。已知沿y轴正方向发射的粒子在t＝t0时刻刚好从磁场边界上P(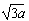，a)点离开磁场．求：
(1)粒子在磁场中做圆周运动的半径R及粒子的比荷q/m；
(2)此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；
(3)从粒子发射到全部粒子离开磁场所用的时间。