1、选择题  如图所示，光滑水平面上有大小相同的A、B两球在同一直线上运动。两球质量关系为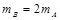，规定向右为正方向，A、B两球的动量均为+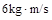，运动中两球发生碰撞，碰撞后A球的动量增量为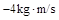，则（?）

A．左方是A球，碰撞后A、B两球速度大小之比为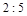
B．左方是A球，碰撞后A、B两球速度大小之比为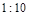
C．右方是A球，碰撞后A、B两球速度大小之比为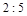
D．右方是A球，碰撞后A、B两球速度大小之比为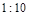

参考答案：A

本题解析：同向运动的两个小球发生碰撞，则后面的小球的速度一定减小，前面的小球速度一定增大，所以左方是Ａ球，右方是Ｂ球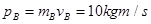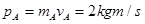，，，又知道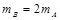，可得碰撞后A、B两球速度大小之比为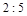，所以Ａ正确。

本题难度：简单

2、选择题  如图所示，物体A静止在光滑的水平面上，A的左边固定有轻质弹簧，与A质量相等的物体B以速度v向A运动并与弹簧发生碰撞，A、B始终沿同一直线运动，则A、B组成的系统动能损失最大的时刻是（　　）

A．开始运动时                         B．A的速度等于v时
C．弹簧压缩至最短时                D．B的速度最小时

参考答案：C

本题解析：试题分析：A、B和弹簧看作糸统只有弹簧弹力做功，所有糸统机械能守恒。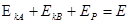，所以当最达时，A、B组成的糸统动能最小。
考点：机械能守恒定律

本题难度：一般

3、简答题  为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞（碰撞过程中没有机械能损失），某同学选取了两个体积相同、质量不等的小球，按下述步骤做了如下实验：
①用天平测出两个小球的质量分别为m1和m2，且m1＞m2．
②按照如图所示的那样，安装好实验装置．将斜槽AB固定在桌边，使槽的末端点的切线水平．将一斜面BC连接在斜槽末端．
③先不放小球m2，让小球m1从斜槽顶端A处由静止开始滚下，记下小球在斜面上的落点位置．
④将小球m2放在斜槽前端边缘处，让小球m1从斜槽顶端A处滚下，使它们发生碰撞，记下小球m1和小球m2在斜面上的落点位置．
⑤用毫米刻度尺量出各个落点位置到斜槽末端点B的距离．图中D、E、F点是该同学记下的小球在斜面上的几个落点位置，到B点的距离分别为LD、LE、LF．
根据该同学的实验，回答下列问题：
（1）小球m1与m2发生碰撞后，m1的落点是图中的______点，m2的落点是图中的______点．
（2）用测得的物理量来表示，只要满足关系式______，则说明碰撞中动量是守恒的．
（3）用测得的物理量来表示，只要再满足关系式______，则说明两小球的碰撞是弹性碰撞．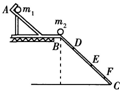

参考答案：（1）小球m1和小球m2相撞后，小球m2的速度增大，小球m1的速度减小，都做平抛运动，所以碰撞后m1球的落地点是D点，m2球的落地点是F点；
（2）碰撞前，小于m1落在图中的E点，设其水平初速度为v1．小球m1和m2发生碰撞后，m1的落点在图中的D点，设其水平初速度为v1′，m2的落点是图中的F点，设其水平初速度为v2． 设斜面BC与水平面的倾角为α，
由平抛运动规律得：LDsinα=12gt2，LDcosα=v′1t
解得：v′1=

本题解析：

本题难度：一般

4、实验题  一个物理学习小组利用图甲所示的装置和频闪相机来探究碰撞中的不变量。其实验步骤如下：

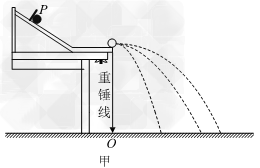
【步骤1】用天平测出A、B两个小球的质量mA、mB（mA>mB）；
【步骤2】安装好实验装置，使斜槽末端保持水平，调整好频闪相机的位置并固定；
【步骤3】让入射小球从斜槽上某一位置P由静止释放，小球离开斜槽后，用频闪相机记录下小球相邻两次闪光时的位置，照片如图乙所示；
【步骤4】将被碰小球放在斜槽末端，让入射小球从位置P由静止开始释放，使它们碰撞。两小球离开斜槽后，用频闪相机记录两小球相邻两次闪光时的位置，照片如图丙所示。

经多次实验，他们猜想碰撞前后物体的质量和速度的乘积之和不变。
（1）实验中放在斜槽末端的小球是__________ （选填“A”、“B”）；
（2）若要验证他们的猜想，需要在照片中直接测量的物理量有_______________（选填“x0”、“y0”、“x1”、“y1”、“x2”、“y2”）。写出该实验小组猜想结果的表达式________________________（用测量量表示）。
（3）他们在课外书中看到，“两物体碰撞中有弹性碰撞和非弹性碰撞之分，碰撞中的恢复系数定义为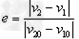，其中v10和v20分别是碰撞前两物体的速度，v1和v2分别是碰撞后两物体的速度，弹性碰撞恢复系数e=1，非弹性碰撞恢复系数e<1。”于是他们根据照片中的信息求出本次实验中恢复系数的值e=___________。（结果保留到小数点后两位数字）

参考答案：（1）B?
（2）x0、x1、x2；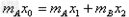
（3）0.88

本题解析：

本题难度：一般

5、简答题  一质量为m的小球以v0的速度与静止在光滑水平面上的质量为M的小球发生对心碰撞，碰撞时无机械能损失.求碰后两球的速度.

参考答案：（1）v1=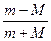v0?⑥
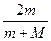v2=v0.?⑦
讨论:（1）m>M时，v1为正；m<M时，v1为负，
即被反向弹回；m=M时，v1=0,v2=v0，即碰后两球交换速度.
（2）当m>>M时，v1≈v0,v2≈2v0;
当m<<M时，v1≈-v0,v2≈0.

本题解析：设碰后m的速度为v1,M的速度为v2,由动量守恒定律得
mv0=mv1+Mv2?①
因碰撞时无机械能损失，总动能守恒
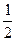mv0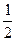2=mv12+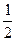Mv22?②
联立求解方程①、②便可得到v1、v2，但该二元二次方程组用代入法解很麻烦，需变形后再解①变为m(v0-v1)=Mv2?③
②变为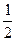m(v02-v12)= 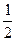Mv22?④
④除以③得
v0+v1=v2?⑤
解①⑤组成的方程组可得v1=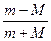v0?⑥
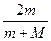v2=v0.?⑦
讨论:（1）m>M时，v1为正；m<M时，v1为负，
即被反向弹回；m=M时，v1=0,v2=v0，即碰后两球交换速度.
（2）当m>>M时，v1≈v0,v2≈2v0;
当m<<M时，v1≈-v0,v2≈0.

本题难度：简单