1、计算题 如图甲所示,光滑水平面上停放着一辆上表面粗糙的平板车,一小金属块以水平速度v0滑到平板车上,在0~t0时间内它们的速度随时间变化的图象如图乙所示,求:
(1)小金属块与平板车的质量之比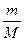 ;
;
(2)小金属块与平板车上表面间的动摩擦因数;
(3)若小金属块刚好没滑离平板车,则平板车的长度为多少。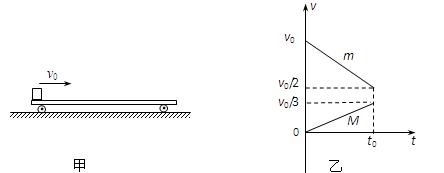
参考答案:(1)以平板车和小金属块为研究对象,由平板车和小金属块组成的系统不受外力,所以动量守恒:
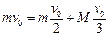 ?代入数据得:?
?代入数据得:? ?(3分)
?(3分)
(2))以小金属块为研究对象,由动量定理
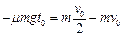 ?代入数据得?
?代入数据得? ?(3分)
?(3分)
(3)设小金属块与平板车最后的共同速度为v,由动量守恒定律:
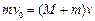 ?代入数据得
?代入数据得 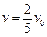 ?(3分)
?(3分)
 ?由能量守恒得
?由能量守恒得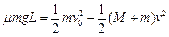 ?
? ?(3分)
?(3分)
本题解析:略
本题难度:一般
2、计算题 (20分)匀强电场的方向沿x轴正向,电场强度E随x的分布如图所示。图中E0和d均为已知量。将带正电的质点A在O点由能止释放。A离开电场足够远后,再将另一带正电的质点B放在O点也由静止释放,当B在电场中运动时,A、B间的相互作用力及相互作用能均为零;B离开电场后,A、B间的相作用视为静电作用。已知A的电荷量为Q,A和B的质量分别为m和 。不计重力。
。不计重力。
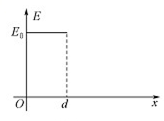
(1)求A在电场中的运动时间t,
(2)若B的电荷量q =  ?Q,求两质点相互作用能的最大值Epm
?Q,求两质点相互作用能的最大值Epm
(3)为使B离开电场后不改变运动方向,求B所带电荷量的最大值qm
参考答案:(1)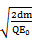 ?(2)
?(2) QE0d?(3)
QE0d?(3) 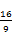 Q
Q
本题解析:解:(1)由牛顿第二定律得,A在电场中的加速度 a = 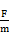 ?=
?= 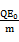
A在电场中做匀变速直线运动,由d =  a
a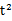 ?得
?得
运动时间 t = 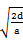 ?=
?= 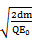
(2)设A、B离开电场时的速度分别为vA0、vB0,由动能定理得
QE0d =  m
m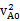
qE0d = 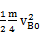
A、B相互作用过程中,动量和能量守恒。A、B相互作用为斥力,A受力与其运动方向相同,B受的力与其运动方向相反,相互作用力对A做正功,对B做负功。A、B靠近的过程中,B的路程大于A的路程,由于作用力大小相等,作用力对B做功的绝对值大于对A做功的绝对值,因此相互作用力做功之和为负,相互作用能增加。所以,当A、B最接近时相互作用能最大,此时两者速度相同,设为v,,
由动量守恒定律得:(m +  )v, = mvA0 +
)v, = mvA0 +  vB0
vB0
由能量守恒定律得:EPm = ( m
m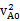 ?+
?+ 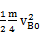 )—
)— )
)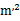
且 q =  Q
Q
解得相互作用能的最大值 EPm =  QE0d
QE0d
(3)A、B在x>d区间的运动,在初始状态和末态均无相互作用
根据动量守恒定律得:mvA +  vB = mvA0 +
vB = mvA0 +  vB0
vB0
根据能量守恒定律得: m
m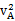 ?+
?+ 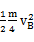 ?=
?=  m
m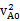 ?+
?+ 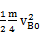
解得:vB = -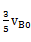 ?+
?+ 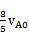
因为B不改变运动方向,所以vB = -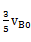 ?+
?+ 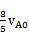 ≥0
≥0
解得: q≤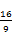 Q
Q
则B所带电荷量的最大值为:qm = 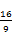 Q
Q
本题难度:一般
3、简答题 如图所示,在高为1.25m的光滑水平台面上放着两个质量分别为0.2kg和0.3kg的小球B、C,两球间用轻质弹簧连接。现有一质量为0.1kg的小球A以v0=10m/s的水平速度与B球在极短的时间内发生正碰并被反弹,A球从水平台上下落后,落地点距平台右边缘的水平距离为1m。已知三个小球半径相同,弹簧的形变在弹性限度内,不计空气阻力,g取10m/s2。求:
(1)碰后小球A的速度;
(2)碰后小球B在压缩弹簧的过程中弹簧的最大弹性势能。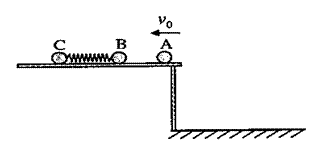
参考答案:(1)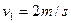 ?(2)
?(2)
本题解析:(1)碰后小球A做平抛运动,设碰后小球A反弹后的速度大小为v1,
水平方向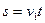 ?①
?①
竖直方向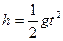 ?②
?②
由①②解得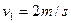 ?③
?③
(2)设碰后小球B的速度大小为v2,碰撞过程时间极短,A、B碰撞动量守恒
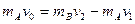 ?④
?④
解得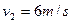
碰后小球B以v2压缩弹簧,当两者速度相同时弹簧的弹性势能最大,设弹性势能最大时B、C的共同速度为v3,根据动量守恒,有:
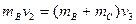 ?⑤
?⑤
解得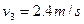
小球B压缩弹簧的过程中,小球B、C和弹簧组成的系统的能量守恒,有:
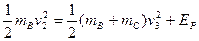 ?⑥
?⑥
解得 ?⑦
?⑦
评分标准:本题满分18分,其中(1)问6分,①②③式各2分;(2)问12分,④⑤⑥⑦式各3分。
本题难度:一般
4、选择题 把一支枪水平固定在小车上,小车放在光滑的水平面上,枪发射出一颗子弹时,关于枪、弹、车,下列说法正确的是
参考答案:
本题解析:
本题难度:一般
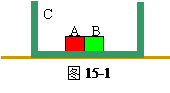
5、简答题 在光滑的水平桌面上有一长L=2米的木板C,它的两端各有一块档板,C的质量mC=5千克,在C的正中央并排放着两个可视为质点的滑块A和B,质量分别为mA=1千克,mB=4千克。开始时,A、B、C都处于静止,并且A、B间夹有少量塑胶炸药,如图15-1所示。炸药爆炸使滑块A以6米/秒的速度水平向左滑动,如果A、B与C间的摩擦可忽略,两滑块中任一块与档板碰撞后都与挡板结合成一体,爆炸和碰撞所需时间都可忽略。
小题1:(1)当两滑块都与档板相碰撞后,板C的速度多大?
小题2:(2)到两个滑块都与档板碰撞为止,板的位移大小和方向如何?
参考答案:
【答案1】C板的速度为零。
【答案2】C的位移为:SC=VCt2=1×0.3=0.3米,方向向左。
本题解析:
【解析1】(1)设向左的方向为正方向。炸药爆炸前后A和B组成的系统水平方向动量守恒。设B获得的速度为mA,则mAVA+mBVB=0,所以:VB=-mAVA/mB=-1.5米/秒对A、B、C组成的系统,开始时都静止,所以系统的初动量为零,因此当A和B都与档板相撞并结合成一体时,它们必静止,所以C板的速度为零。
【解析2】
(2)以炸药爆炸到A与C相碰撞经历的时间:t1=(L/2)/VA=1/6秒,
在这段时间里B的位移为:SB=VBt1=1.5×1/6=0.25米,
设A与C相撞后C的速度为VC,A和C组成的系统水平方向动量守恒:mAVA=(mA+mC)VC,
所以VC=mAVA/(mA+mC)=1×6/(1+5)=1米/秒
B相对于C的速度为: VBC=VB-VC=(-1.5)-(+1)=-2.5米/秒
因此B还要经历时间t2才与C相撞:
t2= =(1-0.25)/2.5=0.3秒,
=(1-0.25)/2.5=0.3秒,
故C的位移为:SC=VCt2=1×0.3=0.3米,
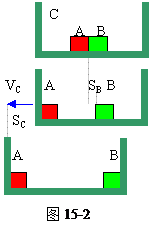
方向向左,如图15-2所示。
本题难度:简单
It is lawful to learn even from an enemy. 向敌人学习不犯法.