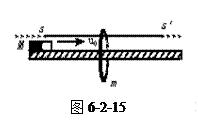
1、选择题 如图6-2-15所示,一根足够长的水平滑杆SS′上套有一质量为m的光滑金属圆环.在滑杆的正下方与其平行放置一足够长的光滑水平的木质轨道,且穿过金属球的圆心O,现使质量为M的条形磁铁以v0的水平速度沿轨道向右运动,则(?)
A.磁铁穿过金属环后,二者将先后停下来
B.圆环可能获得的最大速度为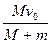
C.磁铁与圆环系统损失的动能可能为Mmv02/2(M+m)
D.磁铁与圆环系统损失的动能可能为 Mv02
Mv02
参考答案:BC
本题解析:整个过程中,二者组成系统总动量守恒,且发生动能向电能再向内能的转化.由动量守恒定律Mv0=(M+m)v,v=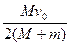 ,又由能量关系:Q=ΔE损=
,又由能量关系:Q=ΔE损= mv02-
mv02- (M+m)v2=
(M+m)v2=
本题难度:一般
2、计算题 如图示,滑板A放在水平面上,长度为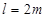 ,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
,滑块质量mA=1 kg、mB=0.99 kg,A、B间粗糙,现有mC="0.01" kg子弹以V0=200m/s速度向右击中B并留在其中,求
(1)子弹C击中B后瞬间,B速度多大
(2)若滑块A与水平面固定,B被子弹击中后恰好滑到A右端静止,求滑块B与A间动摩擦因数μ
(3)若滑块A与水平面光滑,B与A间动摩擦因数不变,试分析B能否离开啊, 并求整个过程A、B、C组成的系统损失的机械能

参考答案:(1)2m/s.(2)0.1.(3)199J
本题解析:(1)子弹 击中
击中 后瞬间,
后瞬间, 速度为
速度为 ,
,
动量守恒: 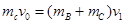 解得:
解得: 
(2)若滑块 与水平面固定,
与水平面固定, 由运动到静止,位移为
由运动到静止,位移为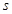 .
.
动能定理有: 

代入数据得: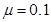
另解:
若滑块 与水平面固定,
与水平面固定, 由运动到静止,位移为
由运动到静止,位移为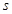 .
.
由牛顿第二定律知:
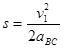

代入数据得: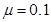
(3)若 与水平面光滑,则
与水平面光滑,则 做匀加速运动,
做匀加速运动,  、
、 做匀减速运动,
做匀减速运动,
 、
、 与
与 间摩擦力:
间摩擦力:
 的加速度大小:
的加速度大小: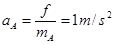
 、
、 的共同加速度大小
的共同加速度大小
设经时间 共速,
共速,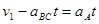 解得:
解得: 
此时 相对
相对 位移:
位移:
因 ,
, 、
、 、
、 最后共速运动,不会分离
最后共速运动,不会分离
所以 滑行最终速度为:
滑行最终速度为: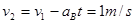
系统损失的机械能为:
另解:
 、
、 与
与 间摩擦力:
间摩擦力:
设 、
、 、
、 最后共速为
最后共速为 ,由动量守恒:
,由动量守恒: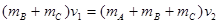
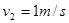
此时 相对
相对 位移为
位移为 ,由功能关系知:
,由功能关系知:

因 ,
, 、
、 、
、 最后共速运动,不会分离
最后共速运动,不会分离
系统损失的机械能为: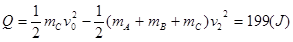
考点:动量守恒定律及能量守恒定律.
本题难度:困难
3、选择题 如图所示,三辆完全相同的平板小车a、b、c成一直线排列,静止在光滑水平面上,c车上有一小孩跳到b车上,接着又立即从b车跳到a车上,小孩跳离c车和b车时对地的水平速度相同,他跳到a车上没有走动便相对a车静止.此后(?)

A.a、c两车运动速率相同
B.三辆车运动速率关系为vc>va>vb
C.a、b两车运动速度相同
D.a、c两车运动方向相同
参考答案:B
本题解析:设人的质量为m,对地速度为v0,车的质量为M.人从c车跳出有:0=mv0-Mvc
人跳到b车再跳出,有mv0=Mvb+mv0
人跳上a车,有mv0=(M+m)va,可得vc>va>vb.
本题难度:简单
4、计算题 如图所示,光滑水平面上有一辆质量为M=1kg的小车,小车的上表面有一个质量为m=0.9kg的滑块,在滑块与小车的挡板间用轻弹簧相连接,滑块与小车上表面间的动摩擦因数为μ=0.2,整个系统一起以v1=10m/s的速度向右做匀速直线运动,此时弹簧长度恰好为原长。现在用一质量为m0=0.1kg的子弹,以v0=50m/s的速度向左射入滑块且不穿出,所用时间极短。当弹簧压缩到最短时,弹簧被锁定,测得此时弹簧的压缩量为d=0.50m,g =10m/s2。求
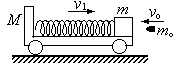
①子弹射入滑块的瞬间,子弹与滑块的共同速度;
②弹簧压缩到最短时,弹簧弹性势能的大小。
参考答案:①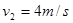 ②
②
本题解析:)①子弹射入滑块后的共同速度大为v2,设向右为正方向,对子弹与滑块组成的系统应用动量守恒定律得
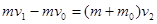 ?①
?①
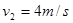 ?②
?②
②子弹,滑块与小车,三者的共同速度为v3,当三者达到共同速度时弹簧压缩量最大,弹性势能最大.由动量守恒定律得
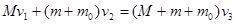 ?③
?③
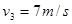 ?④
?④
设最大弹性势能为Epmax,对三个物体组成的系统应用能量守恒定律
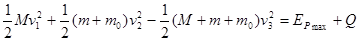 ?⑤
?⑤
 ?⑥
?⑥
由⑤⑥两式解得  ?⑦
?⑦
本题难度:一般
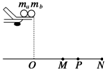
5、填空题 如图所示“为探究碰撞中的不变量”的实验装置示意图.
(1)本实验中,实验必须要求的条件是______
A.斜槽轨道必须是光滑的
B.斜槽轨道末端点的切线是水平的
C.入射小球每次都从斜槽上的同一位置无初速释放
D.入射球与被碰球满足ma>mb,ra=rb
(2)如图,其中M、P、N分别为入射球与被碰球对应的落点的平均位置,则实验中要验证的关系是______
A.ma?ON=ma?OP+mb?OM
B.ma?OP=ma?ON+mb?OM
C.ma?OP=ma?OM+mb?ON
D.ma?OM=ma?OP+mb?ON.
参考答案:(1)A、“验证动量守恒定律”的实验中,是通过平抛运动的基本规律求解碰撞前后的速度的,只要离开轨道后做平抛运动,对斜槽是否光滑没有要求,故A错误;
B、要保证每次小球都做平抛运动,则轨道的末端必须水平,故B正确;
C、要保证碰撞前的速度相同,所以入射球每次都要从同一高度由静止滚下,故C正确;
D、为了保证小球碰撞为对心正碰,且碰后不反弹,要求ma>mb,ra=rb,故D正确.
故选BCD.
(2)要验证动量守恒定律定律即:mav0=mav1+mbv2
小球做平抛运动,根据平抛运动规律可知根据两小球运动的时间相同,上式可转换为:
mav0t=mav1t+mbv2t
故需验证maOP=maOM+mbON,因此ABD错误,C正确.
故选C.
本题解析:
本题难度:一般