1、选择题  “轨道电子俘获”也是放射性同位素衰变的一种形式，它是指原子核（称为母核）俘获一个核外电子，其内部一个质子变为中子，从而变成一个新核（称为子核），并且放出一个中微子的过程，中微子的质量极小，不带电，很难被探测到，人们最早是通过子核的反冲而间接证明中微子的存在的．关于一个静止的母核发生“轨道电子俘获”，衰变为子核并放出中微子，下面的说法中正确的是（　　）
A．子核的动量与中微子的动量相同
B．母核的电荷数小于子核的电荷数
C．母核的质量数等于子核的质量数
D．子核的动能大于中微子的动能

参考答案：A、原子核（称为母核）俘获电子的过程中动量守恒，初状态系统的总动量为0，则子核的动量和中微子的动量大小相等，方向相反．故A错误．
B、原子核（称为母核）俘获一个核外电子，使其内部的一个质子变为中子，并放出一个中微子，从而变成一个新核（称为子核）的过程．电荷数少1，质量数不变．故B错误，C正确．
D、子核的动量大小和中微子的动量大小相等，由于中微子的质量很小，根据EK=P22m知，中微子的动能大于子核的动能．故D错误．
故选C．

本题解析：

本题难度：一般

2、简答题  一个质量为M，底面边长为b的三角形劈块静止于光滑水平面上，如图，有一质量为m的小球由斜面顶部无初速滑到底部的过程中，劈块移动的距离是多少？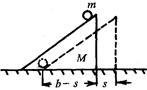

参考答案：s=mb／（M+m）

本题解析：小球m在下滑的过程中，受力情况和速度变化的规律都不易分析，因此用牛顿定律和运动学公式找位移S是困难的；用人船模型的公式解这类求变速直线运动的位移且不涉及速度的问题时，是非常方便的．
解：设小球滑到底端时，劈块后退的位移为S，则小球的水平位移应为（b一S），根据动量守恒定律得Ms=m（b-s），解得劈块移动的距离为s=mb／（M+m）。

本题难度：简单

3、计算题  如图所示，质量M，半径R的光滑半圆槽第一次被固定在光滑水平地面上，质量为m的小球，以某一初速度冲向半圆槽刚好可以到达顶端C．然后放开半圆槽，其可以自由运动，m小球又以同样的初速冲向半圆槽，小球最高可以到达与圆心等高的B点，（g=10m/s2）试求：
①半圆槽第一次被固定时，小球运动至C点后平抛运动的水平射程X=?
②小球质量与半圆槽质量的比值m/M为多少？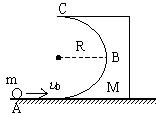

参考答案：①V02=5Rg②m/M=3/2

本题解析：①C点重力提供向心力
由于? mg=mV12/R?（1分） 故有? V1=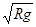?（1分）
m由C点平抛?
Y=2R=gt2/2? (1分)
X=V1t?（1分）
得：X=2R? (1分)
由题意据动能定理可知? V02="5Rg" （1分）
②由题意，对m、M 系统根据动量守恒、能量守恒得
MV0=(m+M)V2?（1分）
MgR=mV02-(m+M)V22?（1分） 得： m/M=3/2?（2分）
点评：难度中等，小球运动到B点时两者速度相同，能够到达C点的临界条件是重力提供向心力

本题难度：一般

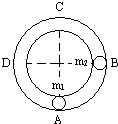
4、选择题  如图所示，在水平桌面上固定着一个光滑圆轨道，在轨道的B点静止着一个质量为m2的弹性小球乙，另一个质量为m1的弹性小球甲以初速v0运动，与乙球发生第一次碰撞后，恰在C点发生第二次碰撞．则甲、乙两球的质量之比m1：m2可能等于（　　）
A．3：5
B．1：9
C．1：7
D．2：3