1、选择题  如图所示，甲、乙两图都在光滑的水平面上，小车的质量都是M，人的质量都是m，甲图人推车，乙图人拉绳子的力都是F，（绳与轮的质量和摩擦均不计），对于甲、乙两车的加速度大小说法正确的是

[? ]
A．甲车的加速度大小为
B．甲车的加速度大小为0
C．乙车的加速度大小为
D．乙车的加速度大小为0

参考答案：BC

本题解析：

本题难度：一般

2、选择题  若带正电荷的小球只受到电场力的作用，它在任意一时间内（　　）
A．一定沿电场线运动
B．一定不沿电场线运动
C．不一定沿电场线运动
D．以上说都不正确

参考答案：只有当电场线是直线时，小球只受到电场力的作用才可能沿电场线运动．若电场线是曲线时，一定不沿电场线运动．题中条件不明，所以小球不一定沿电场线运动．
故选C

本题解析：

本题难度：一般

3、简答题  （附加题，本题不计入总分，仅供同学们思考）如图所示，质量为3m的足够长木板C静
止在光滑水平面上，质量均为m的两个小物体A、B放在C的左端，A、B间相距s0，现同时对A、B施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0，若A、B与C之间的动摩擦因数分别为μ和2μ，则
（1）最终A、B、C的共同速度为多大？
（2）求运动过程中A的最小速度？
（3）A与B最终相距多远？
（4）整个过程中A、B与木板C因摩擦所产生的热量之比为多大？

参考答案：（1）根据动量守恒定律得
? mv0+2mv0=（m+m+3m）v
解得v=0.6v0?
（2）设经过t时间，A与C相对静止，共同速度为vAC，此时B的速度为vB，由动量守恒得
? mv0+2mv0=（m+3m）vAC+mvB
根据动量定理得
? 对A：-μmgt=m（vAC-v0）
? 对C：（μmg+2μmg）t=3mvAC
联立以上三式
? vAC=0.5v0，vB=v0
（3）AC相对静止前，AB做匀减速运动，C做匀加速运动，三个物体的加速度分别为
? aA=μmgm=μg
? aB=2μmgm=2μg
? aC=μmg+2μmg3m=μg
AC相对静止后，AC做匀加速运动，B做匀减速运动，三个物体的加速度分别为
? aA′=aC′=2μmgm+3m=0.5μg
? aB′=aB=2μg
最终三个物体一起做匀速直线运动．
从开始运动到三个物体都相对静止，A、B相对于地的位移分别为
? sA=v20-v2AC2aA+v2-v2AC2aA′=0.485v20μg
? sB=(2v0)2-v22aB=0.91v20μg
所以A与B最终相距△s=s0+sB-sA=s0+0.425v20μg?
（4）设整个运动过程中AC相对于滑行的距离为s，则B相对于C滑行的距离为s+△s-s0．
根据能量守恒定律得
? μmgs+2μmg（s+△s-s0）=12mv20+12m(2v0)2-12(m+m+3m)v2
解得s=s0+0.425v20μg?
整个过程中A、B与木板C因摩擦所产生的热量分别为
? QA=μmgs
? QB=2μmg（s+△s-s0）
代入解得
? QAQB=527
答：
（1）最终A、B、C的共同速度为0.6v0．
（2）运动过程中A的最小速度为0.5v0．
（3）A与B最终相距得s0+0.425v20μg?
（4）整个过程中A、B与木板C因摩擦所产生的热量之比为5：27．

本题解析：

本题难度：一般

4、简答题  如图所示，在0≤x≤a、o≤y≤

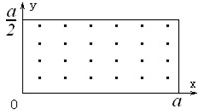
参考答案：

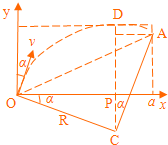
设粒子的发射速度为v，粒子做圆周运动的轨道半径为R，根据洛伦兹力提供向心力，得：
qvB=mv2R
解得
R=mvqB
当a2＜R＜a时，在磁场中运动的时间最长的粒子，其轨迹是圆心为C的圆弧，圆弧与磁场的边界相切，如图所示，设该粒子在磁场中运动的时间为t，依题意，t=T4，回旋角度为∠OCA=π2
设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α，由几何关系得：
Rsinα=R-a2，Rsinα=a-Rcosα，且sin2α+cos2α=1
解得：
R=(2-

本题解析：

本题难度：一般

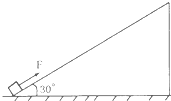
5、简答题  如图所示，一固定粗糙斜面与水平面夹角θ=30°．一质量m=lkg的小物体（可视为质点），在F=10N的沿斜面向上的拉力作用下，由静止沿斜面向上运动．已知斜面与物体间的动摩擦因数μ=

参考答案：（1）力F作用过程，由牛顿第二定律得：
F-mgsinθ-μmgcosθma1，
由匀变速运动的位移公式得：
x1=12a1t2，
物体速度v=a1t，
撤去拉力F后，由牛顿第二定律得：
mgsinθ-μmgcosθ=ma2，
由匀变速运动的速度位移公式得：
x2=0-v2-2a2，
x=x1+x2，
解得：x=5m；
（2）物体返回斜面低端过程中，由动能定理得：
xsinmgsθ-μmgcosθ?x=EK-0，
解得：EK=10J；
答：（1）若力F作用2s后撤去，物体在上滑过程中距出发点的最大距离为5m．
（2）物体再次回到出发点时的动能为10J．

本题解析：

本题难度：一般