1、简答题 据报道,一儿童玩耍时不慎从45m高的阳台上无初速掉下,在他刚掉下时恰被楼下一保安发现,该保安迅速由静止冲向儿童下落处的正下方楼底,准备接住儿童.已知保安到楼底的距离为15m,为确保安全能稳妥接住儿童,保安将尽力节约时间,但又必须保证接儿童时没有水平方向的冲击,不计空气阻力,将儿童和管理人员都看做质点,设保安奔跑过程中是匀变速运动且在加速或减速的加速度大小相等,g取10m/s2,求:
(1)保安跑到楼底的平均速度
(2)保安奔跑时的最大速度
(3)保安加速时的加速度.
2、选择题 做匀加速直线运动的物体初速度为2 m/s,经过一段时间t后速度变为6 m/s,则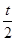 时刻速度为
时刻速度为
A.由于t未知,无法确定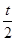 时刻的速度
时刻的速度
B.由于加速度a及时间t未知,无法确定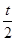 时刻的速度
时刻的速度
C.5 m/s
D.4 m/s
3、选择题 冰壶是冬奥会的比赛项目,冰壶被掷出后在冰面上减速滑行。在一次训练中,通过测量分析后得出它的位移x (m) 随时间t (s) 变化的规律为x =" t" –0.02 t2, 则下列说法正确的是(?)
A.冰壶的加速度大小为0.02m/s2
B.冰壶的初速度为1 m/s
C.5s末冰壶的速度为0.8 m/s
D.30s内冰壶的位移为12m
4、计算题 列车进站前先关闭汽阀,当它匀减速滑行300m时,列车的速度已经减半,以后又继续匀减速速滑行20s后恰好 停于站台上.求列车滑行的总位移和最后10s内的位移.
停于站台上.求列车滑行的总位移和最后10s内的位移.
5、简答题 如图所示,B为位于水平地面上的质量为M的长方形空心盒子,盒内存在着竖直向上场强大小为E=
的匀强电场.A为位于一定高度处的质量为m、带电荷量为+q的小球,且M=2m,盒子与地面间的动摩擦因数μ=0.2,盒外没有电场.盒子的上表面有一些略大于小球直径的小孔,孔间距满足一定的关系,使得小球进出盒子的过程中始终不与盒子接触.当小球A以1m/s的速度从孔1进入盒子的瞬间,盒子B恰以v1=6m/s的速度向右滑行.已知盒子通过电场对小球施加的作用力与小球通过电场对盒子施加的作力大小相等方向相反.设盒子足够长,取重力加速度g=10m/s2,小球恰能顺次从各个小孔进出盒子.试求:
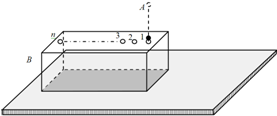
(1)小球A从第一次进入盒子到第二次进入盒子所经历的时间;
(2)盒子上至少要开多少个小孔,才能保证小球始终不与盒子接触;
(3)从小球第一次进入盒子至盒子停止运动的过程中,盒子通过的总路程.