1、选择题  如图所示，在x轴上方存在垂直于纸面向外、磁感应强度为B的匀强磁场．一带电粒子从坐标原点O处以速度v沿y轴正方向进入磁场，最后从P（a，0）射出磁场．不计粒子重力，该带电粒子的电性和比荷

参考答案：由图意可知粒子沿顺时针方向运动，根据左手定则可得粒子带正电
由几何关系得运动半径为：r=a2
由牛顿的定律得：Bqv=mv2r
故有：qm=2vBa
故选C

本题解析：

本题难度：一般

2、填空题  如图所示为研究物质放射性的示意图．铅盒底部装有微量放射性元素，放射源放出的射线在图示水平方向的电场E中分成了a、b、c三束．由图可知射线a是______粒子．射线a在电场中的偏转角明显比射线c的偏转角大，出现这种现象的原因是______．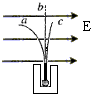

参考答案：α、β和γ三种射线中，α带正电、β带负电、γ不带电．γ射线在电场中不受电场力，不发生偏转．α粒子带正电，所受的电场力水平向右，向右偏转，β粒子所受的电场力水平向左，向左偏转，故射线a是β粒子．
β射线为高速电子流，质量约为质子质量的11800，电量为-e，α粒子的电量为2e．根据牛顿第二定律得知：加速度a=qEm，所以β粒子在水平方向的加速度比较大，偏转角较大．
故答案为：β，β粒子在水平方向的加速度比较大，

本题解析：

本题难度：一般

3、填空题  质量为m，带电量为q的电子以速度v垂直于磁场的方向射入磁感应强度为B的匀强磁场中。则电子作圆周运动的半径为             ；周期为         ；

参考答案：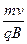  

本题解析：略

本题难度：一般

4、计算题  如图所示，在空间有匀强磁场，磁感应强度的方向垂直纸面向里，大小为B，光滑绝缘空心细管MN的长度为h，管内M端有一质量为m、带正电q的小球P，开始时小球P相对管静止，管带着小球P沿垂直于管长度方向的恒定速度u向右运动。设重力及其它阻力均可忽略不计。求：
（1）当小球P相对管上升的速度为v时，小球上升的加速度多大？
（2）小球P从管的另一端N离开管口后，在磁场中作圆周运动的半径R多大？
（3）小球P在从管的M端到N端的过程中，管壁对小球做的功是多少？

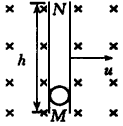
参考答案：解：（1）设此时小球的合速度大小为v合，方向与u的夹角为θ有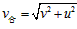①?
cosθ=u/v合=u/ ②
此时粒子受到的洛伦兹力f和管壁的弹力N如图所示，

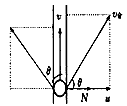
由牛顿第二定律可求此时小球上升的加速度为：a=fcosθ=qv合Bcosθ/m③
联立①②③解得：a=quB/m
（2）由上问可知，小球上升加速度只与小球的水平速度u有关，故小球在竖直方向上做匀加速运动。
设小球离开N端管口时的竖直分速度为vy，由运动学公式得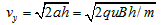
此时小球的合速度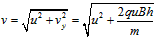
故小球运动的半径为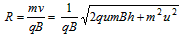
（3）因洛伦兹力对小球做的功为零，由动能定理得管壁对小球做的功为：W= mv2/2－mu2/2=quBh。

本题解析：

本题难度：困难

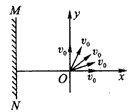
5、计算题  电子质量为m，电荷量为e，从坐标原点O处沿xOy平面射入第一象限，射入时速度方向不同，速度大小均为v0，如图所示。现在某一区域加一方向向外且垂直于xOy平面的匀强磁场，磁感应强度为B，若这些电子穿过磁场后都能垂直射到荧光屏MN上，荧光屏与y轴平行，求：
(1)电子从y轴穿过的范围；
(2)荧光屏上光斑的长度；
(3)所加磁场范围的最小面积。

参考答案：解：(1)设磁场中运动的半径为R ，牛顿第二定律得：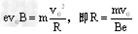
电子从y轴穿过的范围
(2)如图所示，求光斑长度，关键是找到两个边界点，初速度方向沿x轴正方向的电子，沿弧OB运动到P；初速度方向沿y轴正方向的电子，沿弧OC运动到Q
电子在磁场中的半径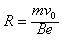
由图可知

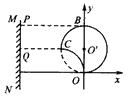
(3)沿任一方向射入第一象限的电子经电场偏转后都能垂直打到荧光屏MN上，所加最小面积的磁场的边界是以O"(0，R)为圆心，R为半径的圆的一部分，如图中实线所示，所以磁场范围的最小面积为

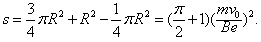
本题解析：

本题难度：困难