1、选择题  一个从地面上竖直上抛的物体，它两次经过一个较低点A的时间间隔是5 s，两次经过一个较高点B的时间间隔是3 s，则AB之间的距离是（g="10" m/s2）（?）
A．80 m
B．40 m
C．20 m
D．初速未知，无法确定

参考答案：C

本题解析：略

本题难度：简单

2、简答题  原地起跳时，先曲腿下蹲，然后突然蹬地．从开始蹬地到离地是加速过程（视为匀加速），加速过程中重心上升的距离称为“加速距离”．跳蚤原地起跳的“加速距离”d1=0.00075m，离地时速度大小v1=1.5m/s．
（1）求跳蚤起跳过程中的加速度大小是多少？
（2）人原地起跳的“加速距离”d2=0.3m，假想人具有跳蚤相等的起跳加速度，则人跳离地面时的速度大小是多少？
（3）若人以此速度离开地面后，做加速度大小为10m/s2的匀减速运动，则人离地后上升的最大高度是多少？

参考答案：（1）跳蚤起跳过程是匀加速直线运动，根据速度位移关系公式，有：
v12=2ad1
解得：a=v122d1=1．522×0.00075=1500m/s2
（2）人起跳过程是匀加速直线运动，根据速度位移关系公式，有：
v22=2ad2
解得：v2=

本题解析：

本题难度：一般

3、计算题  （16分）节日燃放的烟花弹射到最高点爆炸散开形成多彩绚丽的景色，给节日增添了几分喜庆．在2010年除夕夜的重庆某地，某人在观看竖直发射的烟花时，看到烟花爆炸时的视线与水平方向夹角为530，看见爆炸到听见爆炸声的间隔时间是1.5s，设烟花燃放点与观察者在同一水平面上，不计空气阻力，忽略光在空中传播时间和观察者高度．（己知sin530 = 0.8，cos530 = 0.6，声速vo = 340m/s，g = 10m/s2）．求：
（1）烟花燃放点与观察者问的水平距离；
（2）烟花爆炸点距地面高度；
（3）烟花弹射离地时的速度．

参考答 案：（1）510m
（2）408m
（3）90m/s

本题解析：
（1）烟花爆炸位置与观察者闻的直线距离为
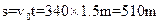?（4分）
由几何关系可知，烟花燃放点与观察者问的水平距离
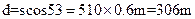?（4分）
（2）烟花弹射的竖直高度为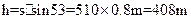?（4分）
（3）烟花弹射离地时的速度为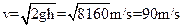?（4分）

本题难度：一般

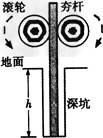
4、计算题  如图所示是建筑工地常用的一种“深穴打夯机”。工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯从深为h的坑中提上来，当两个滚轮彼此分开时，夯杆被释放，最后夯在自身重力作用下，落回深坑，夯实坑底。然后，两个滚轮再次压紧，夯杆再次被提上来，如此周而复始工作。已知两个滚轮边缘线速度v恒为4 m/s，每个滚轮对夯杆的正压力FN为2×104N，滚轮与夯杆间的动摩擦因数为0.3，夯杆质量m为1×103 kg，坑深h为6m。假定在打夯的过程中坑的深度变化不大，且夯杆底端升到坑口时，速度正好为零，取g=10m/s2，求：
(1)每个打夯周期中，电动机对夯杆所做的功；
(2)夯杆上升过程中被滚轮释放时夯杆底端离坑底多高；
(3)打夯周期。

参考答案：解：(1)因为夯杆底端升到坑口时，速度正好为零，所以每个打夯周期中，电动机对夯杆所做的功W=mgh=6×104 J?
(2)根据题意，考虑到夯杆先匀加速上升，后匀速上升，再竖直上抛
当夯杆以v=4 m/s的初速度竖直上抛，上升高度为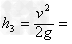：0.8 m
此时夯杆底端离坑底△h=h-h3=5.2 m
(3)以夯杆为研究对象f1=2μN=1.2×104 N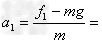；2m/s2
当夯杆与滚轮相对静止时：v=a1t1=4m/s，t1=2s，h1=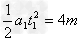
则当夯杆加速向上运动速度达到v=4 m/s后，夯杆匀速上升，匀速上升高度为：h2=h-h1-h3=1.2m
因此，夯杆上抛运动的时间为：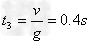
夯杆匀速上升的时间为：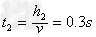
夯杆自由落体的时间为：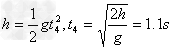
故打夯周期为：T=t1+t2+t3+t4=3.8 s

本题解析：

本题难度：困难

5、计算题  某同学拍一个可视为质点、质量为m=0.1kg的橡皮小球，使它在距地面高h1=0.8m的范围内做竖直方向的往复运动，在球到最高点时用手开始击打球，手与球作用过程中球下降了h2=0.05m，球从落地到反弹离地历时t=0.1s，球反弹离地时的速度大小v2是刚触地时的速度大小v1的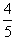，且反弹恰好到最高点。若手对球和地面对球的作用力均可视为恒力，忽略空气阻力，g取10m/s2。试求：
（1）球反弹离地的速度大小v2；
（2）地面对球弹力大小FN；
（3）拍球时手对球作用力大小F。

参考答案：解：（1）球反弹离地后做竖直上抛运动，有

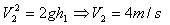
故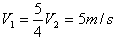
（2）以竖直向上为正方向，球从落地到反弹离地过程中，由动量定理：

?（3）从开始拍球到球刚触地过程，由动能定理：

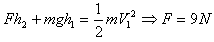
本题解析：

本题难度：困难