1、计算题  如图（a）所示的螺线管，匝数n=1500匝，横截面积S=20cm2,电阻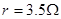，与螺线管串联的外电阻，。方向向左，穿过螺线管的匀强磁场的磁感应强度按图（b）所示规律变化，求：
（1）电阻R2的电功率；
（2）a、b两点的电势（设c点电势为零）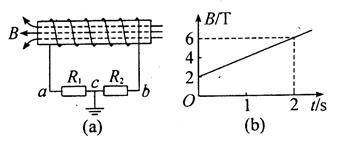

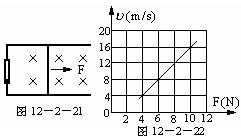
2、简答题  水平向上足够长的金属导轨平行固定放置，间距为L，一端通过导线与阻值为R的电阻连接；导轨上放一质量为m的金属杆（如图12－2－21所示），金属杆与导轨的电阻忽略不计；均匀磁场竖直向下．用与导轨平行的恒定拉力F作用在金属杆上，杆最终将做匀速运动．当改变拉力大小时，相对应的匀速运动速度也会变化，和F的关系如图12－2－22所示．（取重力加速度）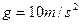

（1）金属杆在匀速运动之前做什么运动？
（2）若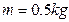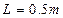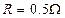，，；磁感应强度B为多大？
（3）由－F图线的截距可求得什么物理量？其值为多少？

3、简答题  如图所示，两根间距为L的金属导轨MN和PQ，电阻不计，左端弯曲部分光滑，水平部分导轨与导体棒间的滑动摩擦因数为μ，水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ，右端有另一磁场Ⅱ，其宽度也为d，但方向竖直向下，两磁场的磁感强度大小均为B0，相隔的距离也为d．有两根质量为m、电阻均为R的金属棒a和b与导轨垂直放置，b棒置于磁场Ⅱ中点C、D处．现将a棒从弯曲导轨上某一高处由静止释放并沿导轨运动下去．
（1）当a棒在磁场Ⅰ中运动时，若要使b棒在导轨上保持静止，则a棒刚释放时的高度应小于某一值h0，求h0的大小；
（2）若将a棒从弯曲导轨上高度为h（h＜h0）处由静止释放，a棒恰好能运动到磁场Ⅱ的左边界处停止，求a棒克服安培力所做的功；
（3）若将a棒仍从弯曲导轨上高度为h（h＜h0）处由静止释放，为使a棒通过磁场Ⅰ时恰好无感应电流，可让磁场Ⅱ的磁感应强度随时间而变化，将a棒刚进入磁场Ⅰ的时刻记为t=0，此时磁场Ⅱ的磁感应强度为B0，试求出在a棒通过磁场Ⅰ的这段时间里，磁场Ⅱ的磁感应强度随时间变化的关系式．

4、简答题  如图所示，平行光滑导轨OPQ、OˊPˊQˊ相距L=0.5m，导轨平面与水平面成θ=53°角，OP段和OˊPˊ段是导电的，PQ段和PˊQˊ段是绝缘的，在P和Pˊ处固定一个“∩”形导体框abcd，导体框平面与导轨面垂直，面积S=0.3m2．空间存在变化的匀强磁场，方向与导轨平行，与线圈abcd垂直．质量为m=0.02kg、电阻R=0.2Ω的金属棒AB放在两导轨上QQˊ处，与PPˊ的距离x=0.64m，棒与导轨垂直并保持良好接触．t=0时刻，从QQˊ无初速度释放金属棒AB，此时匀强磁场方向沿导轨向上（规定为正方向），磁感应强度B的变化规律为B=0.2-0.8t（T）．除金属棒AB外，不计其它电阻．求：
（1）经过多长时间，金属棒AB中有感应电流？感应电流的方向如何？
（2）假设OP段和OˊPˊ段的导轨足够长，金属棒AB在OP段和OˊPˊ段的导轨上能滑行多远？
（sin53°=0.8，cos53°=0.6，g取10m/s2）

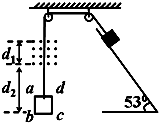
5、简答题  如图，一边长L=0.4m、质量m1=0.2kg、电阻R=0.1Ω的正方形导体线框abcd，与一质量为m2=1.0kg的物块通过轻质细线跨过两定滑轮相连．磁感应强度B=1.0T，磁场宽度d1=0.8m，开始时bc边距磁场下边界为d2=1.0m，物块放在倾角θ=53°的斜面上，物块与斜面间的动摩擦因数为μ=