1、计算题  如图所示，ABC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合。现有一质量为m=1kg可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，
（1）若要使小球经C处水平进入轨道DEF且能沿轨道运动，H至少要有多高？
（2）若小球静止释放处离C点的高度h小于（1）中H的最小值，小球可击中与圆心等高的E点，求h。（取g=10m/s2）
（3）若小球自H=0.3m处静止释放，求小球到达F点对轨道的压力大小。

参考答案：（1）0.2 m
（2）0.1 m
（3）65N

本题解析：

本题难度：困难

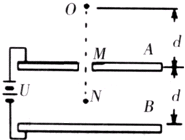
2、简答题  如图，A．B为平行板电容器，两板相距d，接在电压为U的电源上，在A板的中央有一小孔M（两板间电场可视为匀强电场）．今有一质量为m的带电质点，自A板上方与A板相距也为d的O点由静止自由下落，穿过小孔M后到达距B板

参考答案：（1）质点先做自由落体运动到M点，到达N处时速度恰好为零，说明在MN间做减速运动，
合外力向上，所以电场力方向向上，而电场强度方向向下，所以质点带负电；
两极板间的场强E：U=Ed ①，
设电量大小为q，则从O到N点，
由动能定理可得：mg(d+d2)-Eqd2=0②，
由①②解得：q=3mgdU ③；
（2）当A板下移d4时，两板间的距离d′=d-d4=3d4④，
两板间的场强E"：U=E′d′⑤，
设下落速度为零时距B板距离为△d，
从开始下落到速度为零的过程中，
由动能定理得：mg(2d-△d)-E′q(3d4-△d)=0 ⑥，
由③④⑤⑥解得：△d=d3；
答：（1）带电质点的电荷量为3mgdU，质点带负电；
（2）质点下落速度为零时距B板的距离为d3．

本题解析：

本题难度：一般

3、选择题  把导体匀速拉上斜面，如图所示，则下列说法正确的是（不计棒和导轨的电阻，且接触面光滑，匀强磁场磁感应强度B垂直框面向上）（?）

A．拉力做的功等于棒的机械能的增量
B．拉力对棒做的功等于棒的动能的增量
C．拉力与棒受到的磁场力的合力为零
D．拉力对棒做的功与棒克服重力做的功之差等于回路中产生电能

参考答案：D

本题解析：
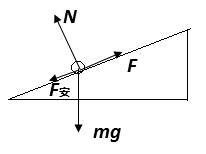受力分析如图所示，由能量守恒定律知，拉力和安培力做功的代数和等于棒的机械能的增量，所以A选项错误；合外力做的功等于动能的变化，即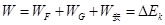，所以B选项错误；拉力、重力、支持力及棒受到的磁场力的合力为零，C选项错误；把导体匀速拉上斜面，由动能定理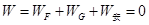，所以拉力对棒做的功与棒的重力做的功的代数和等于物体克服安培力所做的功，而克服安培力所做的的功等于回路中产生电能，故D选项正确。

本题难度：一般

4、计算题  如图所示，半径R=2m的四分之一粗糙圆弧轨道AB置于竖直平面内，轨道的B端切线水平，且距水平地面高度为h=1.25m，现将一质量m=0.2kg的小滑块从A点由静止释放，滑块沿圆弧轨道运动至B点以v=5m/s的速度水平飞出（g取10m／s2）。求：
（1）小滑块沿圆弧轨道运动过程中所受摩擦力做的功；
（2）小滑块经过B点时对圆轨道的压力大小；
（3）小滑块着地时的速度大小。

参考答案：解：（1）由动能定理有mgR+Wf=
得Wf=-1.5J
（2）设轨道对滑块的支持力为N，由牛顿第二定律有N－mg=
得N=4.5N
由牛顿第三定律知滑块对B的压力为4.5N，方向竖直向下
（3）滑块过B点后作平抛运动，设着地时竖直速度为vy，有
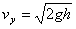=5m/s
所以

本题解析：

本题难度：一般

5、选择题  质量为m的跳水运动员，从离水面高h的跳台上以速度v1斜向上跳起，跳起的最大高度为H（离跳台），最后又以速度v2进入水池中，不计空气阻力，则运动员起跳时所做的功是
A．mg（H+h）
B．
C．+mgh
D．+mgh

参考答案：B

本题解析：运动员起跳时所做的功为其动能的增加量，所以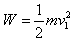，故选B
点评：用动能定理列式，要能灵活的选择运动过程，通常过程选择的越大，解题过程越简单．

本题难度：简单