1、填空题  如图所示，粗细均匀的、电阻为r的金属圆环，放在图示的匀强磁场中，磁感应强度为B，圆环直径为l；长为l、电阻为

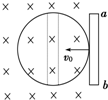
参考答案：当ab棒以v0向左运动到图示虚线位置时产生的感应电动势为：E=BLv0，外电路总电阻为：R=r2×r2r2+r2=14r，
金属棒两端的电势差是外电压，由欧姆定律得金属棒两端电势差为：U=IR=ER+r2R=BLv014r+r2×14r=13BLv0．
故答案为：13BLv0．

本题解析：

本题难度：一般

2 、简答题  如图甲所示，两根足够长的平行导轨处在与水平方向成θ角的斜面上，θ=370，导轨电阻不计，间距L=0.3m．在斜面上加有磁感应强度B=1T、方向垂直于导轨平面向上的匀强磁场．导轨底端接一个阻值R=1Ω的电阻．质量m=1kg、电阻r=2Ω的金属棒ab横跨在平行导轨间，棒与导轨间的动摩擦因数μ=0.5，金属棒从距底端高为h1=2.0m处以平行于导轨向上的初速度v0=10m/s上滑，滑至最高点时高度为h2=3.2m，sin37°=0.6，cos37°=0.8，取g=10m/s2．
（1）求ab棒上升至最高点的过程中，通过电阻R的电量q和电阻R产生的焦耳热Q．
（2）若ab棒固定在导轨上的初始位置，磁场按图乙所示规律变化（2.5×10-2～7.5×10-2s内是正弦规律变化），电阻R在一个周期内产生的焦耳热为Q=5J，取π2=10，求B0．

参考答案：（1）ab棒上升至最高点的过程中，由电量q=It，
闭合电路欧姆定律，I=ER+r
产生感应电动势，E=N△?△t
则通过电阻R的电量：
q=△?R+r=BLXR+r=1×0.3×1.2/0.63=0.2c
ab棒上升至最高点的过程中，由能量守恒定律可得：
12mv20=mg(h2-h1)+μmgcos370(h2-h1)sin370+Q
解之得：Q=30J
电阻R上的热量：QR=Q3=10J
（2）在0～T4内，E1=B0T/4S=4B0T=40B0
I1=E1R+r=40B03
Q1=I21RT4=40B209
在T4～T2内，E2m=B0Sω=2πB0ST
E2=2πB0S

本题解析：

本题难度：一般

3、选择题  如图所示，两根足够长光滑平行金属导轨PQ、MN倾斜固定，倾角为θ=30°，相距为L，导轨处于磁感应强度为B、方向垂直导轨平面向下的匀强磁场中。有两根质量均为m的金属棒a、b，先将a棒垂直导轨放置，用跨过光滑定滑轮的细线与小球c连接，连接a棒的细线平行于导轨，由静止释放c，此后某时刻，将b棒也垂直导轨放置在导轨上，b刚好能静止。a棒在运动过程中始终与导轨垂直，两棒与导轨接触良好，导轨电阻不计，重力加速度为g。则

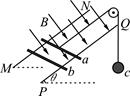
A．小球c的质量为m
B．b棒放上导轨前a棒的加速度为0.5g
C．b棒放上导轨后a棒中电流大小是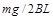
D．b棒放上导轨后，小球c减少的重力势能等于回路消耗的电能

参考答案：AC

本题解析：b棒静止说明b棒受力平衡，即安培力和重力沿斜面向下的分力平衡，此时a棒匀速向上运动，说明a棒受绳的拉力和重力沿斜面向下的分力大小以及沿斜面向下的安培力三个力平衡，c匀速下降，则c所受重力和绳的拉力大小平衡．由b平衡可知，安培力大小F安=mgsinθ，由a平衡可知F绳=F+mgsinθ=2mgsinθ，由c平衡可知F绳=mcg；因为绳中拉力大小相等，故2mgsinθ=mcg，即物块c的质量为2msinθ=m，故A正确；根据BIL= mgsin300，可知b棒放上导轨后a棒中电流大小是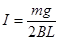，选项C正确；b棒放上导轨后，小球c减少的重力势能等于a增加的重力势能与回路消耗的电能之和，选项D错误；b棒放上导轨前a棒的加速度为=2ma，解得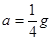，选项B错误；故选AC。
考点：法拉第电磁感应定律；物体的平衡。

本题难度：困难

4、简答题  如图所示，在一磁感应强度B=0.5T的匀强磁场中，垂直于磁场方向水平放置着两根相距为h=0.1m的平行金属导轨MN和PQ，导轨电阻忽略不计，在两根导轨的端点N、Q之间连接一阻值R=0.3Ω的电阻．导轨上跨放着一根长为L=0.2m，每米长电阻r=2.0Ω/m的金属棒ab，金属棒与导轨正交放置，交点为c、d，当金属棒在水平拉力作用于以速度v=4.0m/s向左做匀速运动时，试求：
（1）使金属棒做匀速运动的拉力；
（2）回路中的发热功率；
（3）金属棒ab两端点间的电势差．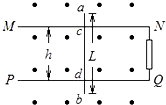

参考答案：（1）金属棒cd段产生的感应电动势为Ecd=Bhv=0.5×0.1×4=0.2V
cdQN中产生的感应电流为? I=EcdR+hr=0.20.3+0.2A=0.4A
使金属棒匀速运动的外力与安培力是一对平衡力，方向向左，大小为
? F=F安=BIh=0.5×0.4×0.1N=0.02N
（2）回路中的热功率P热=I2（R+hr）=0.08W
（3）金属棒ab两端的电势差等于Uac、Ucd、Udb三者之和，由于
? Ucd=Ecd-Ircd，
所以 Uab=Eab-Ircd=BLv-Ircd=0.32v．
答：
（1）使金属棒做匀速运动的拉力是0.02N；
（2）回路中的发热功率为0.08W；
（3）金属棒ab两端点间的电势差是0.32v．

本题解析：

本题难度：一般

5、选择题  如图所示，外力F使金属杆ab在匀强磁场中沿光滑水平金属导轨作匀速运动，除电阻R外，其它电阻均忽略．若下列各种情况中杆ab都能保持匀速运动状态，则（　　）
A．当F一定时，R减小为原来的一半，则F的功率也减小为原来的一半
B．当F一定时，为使杆的速度增大为原来的2倍，必须使R也增大为原来的2倍
C．当F的功率一定时，要使F能增大为原来的2倍，应使R减小为原来的一半
D．若R不变，当F增大为原来的2倍时，杆的速度也应增大到原来的2倍