1、简答题  物体作匀加速直线运动，初速度为8m/s，加速度为5m/s2，求物体10s末的速度和10s内的位移．

参考答案：（1）根据匀加速运动速度公式得：vt=v0+at=8+10×5m/s=58m/s；
（2）由位移公式得：x=v0t+12at2=8×10+12×5×102m=330m；
答：（1）10s末的速度大小为58m/s；
（2）10s内的位移大小为330m．

本题解析：

本题难度：一般

2、选择题  一质点做匀加速直线运动，依次通过A、B、C三点，BC段的长度是AB段的长度的两倍，且质点在AB段的平均速度是3m/s，质点在BC段的平均速度是6m/s，则质点在B点的瞬时速度为(? )
A.4m/s? B. 4.5m/s? C. 5m/s? D.5.5m/s

参考答案：B

本题解析：设A到B的运动时间为t1,B到C的运动时间为t2,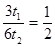,可得t1=t2，可知B点为AC的中间时刻，根据中间时刻的瞬时速度等于平均速度可知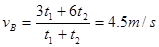，B对；

本题难度：简单

3、选择题  在平直的轨道上，甲、乙两车相距为s，同向同时开始运动．甲在后做初速度为v1，加速度为a1的匀加速直线运动，乙在前做初速度为零，加速度为a2的匀加速直线运动．假定甲能从乙的旁边通过而互不影响，下列情况可能发生的是（　　）
A．a1=a2时，甲、乙只能相遇一次
B．a1＞a2时，甲、乙可能相遇二次
C．a1＞a2时，甲、乙只能相遇一次
D．a1＜a2时，甲、乙可能相遇二次

参考答案：ACD

本题解析：

本题难度：一般

4、选择题  某一做匀变速直线运动的质点的位移随时间的变化的关系式为s＝4t＋2t2，s与t的单位分别为m与s，则质点的初速度与加速度分别为：（?）
A．4m/s与2m/s2
B．0与4m/s2
C．4m/s与4m/s2
D．4m/s与0

参考答案：C

本题解析：匀变速直线运动物体的位移随时间变化的公式为
该题中位移随时间的变化的关系式可写为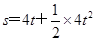，一一对应可得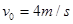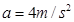，，所以C正确，
点评：本题的关键是正确掌握公式，是一道非常好的题目，比较简单

本题难度：一般

5、简答题  甲、乙两车在一条直线上沿相同方向运动，甲在乙前x=56m处，甲以初速度v1=16m/s、加速度大小为a1=2m/s2匀减速刹车，乙以初速度v2=4m/s、加速度大小为a2=1m/s2做匀加速运动，求：
（1）乙车追上甲车前二者间的最大距离；
（2）乙车追上甲车所需时间．

参考答案：（1）在开始阶段甲车在前、乙车在后，且甲车速度比乙车大，两车距离一直增大，设运动时间为?t?时速度相同，设为v，
应用速度公式v=v0+at，有v1-a1t=v2+a2t
代入数据解得t=4s，v=v1-a1t=8m/s．
此后甲车减速、乙车还在加速，两车距离缩短，所以在速度相等时两车距离最大，
最大距离为△x=x+x1-x2=56m+v2-v12-2a1-v2-v222a2=80m．
（2）甲车停下还需时间为t2=0-v-a1=4s，运动位移为x3=0-v2-2a1=16m．
在此时间内乙车位移为x4=vt2+12a2t22=40m．
显然此时乙车还没有追上甲车，此后甲车停止运动，设乙车追上甲车需时间为t1，则有x+0-v12-2a1=v2t1+12a2t12
联立解得t1=12s．
答：（1）乙车追上甲车前二者间的最大距离为80m．
（2）乙车追上甲车所需时间为12s．

本题解析：

本题难度：一般