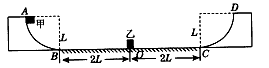
1、计算题 如图所示的凹形场地,两端是半径为L的光滑1/4圆弧面,中间是长为4L的粗糙水平面,质量为3m的滑块乙开始停在水平面的中点0处,质量为m的滑块甲从光滑圆弧面顶端A处无初速度滑下,进入水平面内并与乙发生碰撞,碰后以碰前一半的速度反弹。已知甲、乙与水平面的动摩擦因数分别为μ1,μ2且μ1= 2μ2。甲、乙的体积大小忽略不计,求:
(1)甲与乙碰撞前的速度。
(2)碰后瞬间乙的速度。
(3)甲、乙在O处发生碰撞后,刚好不再发生碰撞,则甲、乙停在距B点多远处。
参考答案:解:(1)设甲到达O处与乙碰撞前的速度为v甲,由动能定理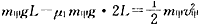
得 ?
?
(2)设碰撞后甲乙速度为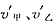 ,则
,则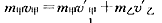
又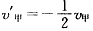 ,得:
,得: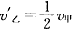 。
。
?(3)由于μ1=2μ2,所以甲、乙在水平面上运动的加速度满足:a甲=2a乙
设甲在水平地面上通过的路程为S1、乙在水平地面上通过的路程为S2,则有:v"甲2=2a甲1
v"乙2=2a乙S2,即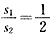 ①
①
由于甲、乙刚好不再发生第二次碰撞,所以甲、乙在同一地点停下。
有以下两种情况:
第一种情况:甲返回时未到达B时就已经停下,此时有:S1<2L
而乙停在甲所在位置时,乙通过的路程为:S2=2L+2L+S1=4L+S1
因为S1与S2不能满足①,因而这种情况不能发生。
第二种情况:甲、乙分别通过B、C冲上圆弧面后,返回水平面后相向运动停在同一地点,
所以有:S1+S2=8L②
由①②两式得:
即小车停在距B为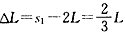 。
。
本题解析:
本题难度:困难
2、填空题 如图所示,质量为M的车厢静止在光滑的水平面上,车厢内有一质量为m的滑块,以初速度v0在车厢地板上向右运动,与车厢两壁发生若干次碰撞,最后静止在车厢中,则车厢最终的速度大小______________,此过程中损失的机械能_______________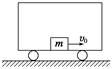
参考答案: ?
?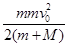
本题解析:以整体为研究对象,系统动量守恒,所以 ,则车厢最终的速度大小为
,则车厢最终的速度大小为 ,此过程中损失的机械能
,此过程中损失的机械能
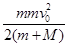
故答案为: ,
,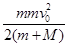
本题难度:简单
3、选择题 如图所示,一质量M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一个质量m=1.0kg的小木块A.给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动, A始终没有滑离B板.在小木块A做加速运动的时间内,木板速度大小可能是 。

A.1.8m/s B.2.4m/s C.2.8m/s D.3.0m/s
参考答案:B
本题解析:取水平向右方向为正方向,当A的速度为零,根据动量守恒定律得:
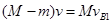
解得:
当AB速度相同时,根据动量守恒定律得:
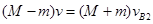
解得:
则在木块A正在做加速运动的时间内,木板的速度范围为:
所以正确选项为B。
考点:本题考查了动量守恒定律的应用。
本题难度:一般
4、选择题 在光滑的水平面上,质量为m的A球以速度v0与质量为2m的静止B球发生对心碰撞,碰后A球的速率变为碰前的
,则碰后B球的速度大小为( )
A.v0
B.v0
C.v0
D.v0
参考答案:若碰后A球速度方向和原来一致,则根据动量守恒得:mv0=mv1+2mv2
将v1=v03带入得v2=2v06=v03;
若碰后A球速度方向和原来相反,则根据动量守恒得:
?mv0=mv1+2mv2
将v1=-v03带入公式得:v2=23v0
故选AB.
本题解析:
本题难度:一般
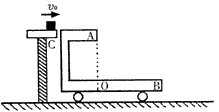
5、计算题 如图所示,在光滑的水平面上停放着一辆质量为M的小车,小车上的平台是粗糙的,停在光滑的水平桌面旁。现有一质量为m的质点C以初速度v0沿水平桌面向右运动,滑上平台后从A端点离开平台,并恰好落在小车的前端B点。此后,质点C与小车以共同的速度运动。已知OA=h,OB=s,则:
(1)质点C刚离开平台A端时,小车获得的速度多大?
(2)在质点C与小车相互作用的整个过程中,系统损失的机械能是多少?
参考答案:解:(1)设质点C离开平台时的速度为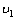 ,小车的速度为
,小车的速度为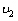 ,对于质点C和小车组成的系统,动量守恒:m
,对于质点C和小车组成的系统,动量守恒:m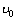 =m
=m +M
+M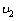 ①
①
从质点C离开A后到还未落在小车上以前,质点C作平抛运动,小车作匀速运动,则:
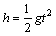 ②,
②, ③
③
由①、②、③式解得:
(2)设小车最后运动的速度为 ,在水平方向上运用动量守恒定律:m
,在水平方向上运用动量守恒定律:m =(M+m)
=(M+m)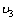 ④
④
设OB水平面的重力势能为零,由能量守恒定律得 ⑤
⑤
由④、⑤两式解得
本题解析:
本题难度:困难