1、简答题  两个氘核聚变产生一个中子和氦核（氦的同位素）．已知氘核的质量mD=2.01360u，氦核的质量mHe=3.0150u，中子的质量mn=1.0087u．
（1）写出聚变方程并计算释放的核能．
（2）若反应前两个氘核的动能为0.35Mev．它们正面对撞发生聚变，且反应后释放的核能全部转化为动能，则产生的氦核和中子的动能各为多大？

参考答案：（1）聚变的核反应方程：212H→23He+01n
核反应过程中的质量亏损为△m=2mD-（mHe+mn）=0.0035u
释放的核能为△E=△mc2=0.0035uc2=3.26MeV?
（2）对撞过程动量守恒，由于反应前两氘核动能相同，其动量等值反向，因此反应前后系统的动量为0．即：
0=mHevHe+mnvn，
反应前后总能量守恒，得：
12mHevHe2+12mnvn2=△E+2Ek0，
解得：EkHe=0.99Mev，Ekn=2.97Mev．?
答：（1）聚变的核反应方程：212H→23He+01n，释放的核能为3.26MeV；?
? ?（2）产生的氦核的动能为0.99Mev，中子的动能为2.97Mev．

本题解析：

本题难度：一般

2、简答题  如图所示，质量M=1.5kg的小车静止于光滑水平面上并紧靠固定在水平面上的桌子右边，其上表面与水平桌面相平，小车的左端放有一质量为0.5kg的滑块Q．水平放置的轻弹簧左端固定，质量为0.5kg的小物块P置于光滑桌面上的A点并与弹簧的右端接触，此时弹簧处于原长．现用水平向左的推力F将P缓慢推至B点（弹簧仍在弹性限度内），推力做功WF=4J，撤去F后，P沿桌面滑到小车左端并与Q发生弹性碰撞，最后Q恰好没从小车上滑下．已知Q与小车表面间动摩擦因数μ=0.1．（g=10m/s2）求：
（1）P刚要与Q碰撞前的速度是多少？
（2）Q刚在小车上滑行时的初速度v0是多少？
（3）为保证Q不从小车上滑下，小车的长度至少为多少？

参考答案：（1）推力F通过P压缩弹簧做功，根据功能关系有：EP=WP…①
当弹簧完全推开物块P时，有：EP=12mPv2… ②
由①②式联立解得：v=4 m/s
（2）选取P与Q组成的系统为研究的对象，P运动的方向为正方向，则P、Q之间发生弹性碰撞，设碰撞后Q的速度为v0，P的速度为v′，由动量守恒和能量守恒得：
mPv=mpv′+mQv0…③
12mpv2=12mpv′2+12mQv2Q ④
由③④式解得：v0=v=4m/s，v′=0
（3）设滑块Q在小车上滑行一段时间后两者的共同速度为u，由动量守恒可得：
mQv0=（mQ+M）u…⑤
根据能量守恒，系统产生的摩擦热：
μmQgL=12mQv20-12(mQ+M)u2…⑥
联立⑤⑥解得：L=6m
答：（1）P刚要与Q碰撞前的速度是4m/s；
（2）Q刚在小车上滑行时的初速度v0是4m/s；
（3）为保证Q不从小车上滑下，小车的长度至少为6m．

本题解析：

本题难度：一般

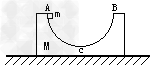
3、选择题  如图所示，在光滑的水平面上有一物体M，物体上有一光滑的半圆弧轨道，最低点为C，两端A、B一样高。现让小滑块m从A点静止下滑，则

[? ]
A．m不能到达小车上的B点
B．m从A到C的过程中M向左运动，m从C到B的过程中M向右运动
C．m从A到B的过程中小车一直向左运动，m到达B的瞬间，M速度为零
D．M与m组成的系统机械能守恒，动量守恒

参考答案：C

本题解析：

本题难度：一般

4、简答题  ［物理——选修3－5］
（1）（5分）以下说法中正确是?（填选项前的字母）
A．光电效应现象表明光具有波动性
B．贝克勒尔发现了铀和含铀矿物的天然放射现象
C．利用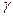射线的电离作用，可检查金属内部有无砂眼或裂纹
D．氢原子的能级图如图所示，欲使一处于基态的氢原子释放出一个电子而变成氢离子，该氢原子需要吸收的能量至少是13．60eV