1、简答题  在牛顿发现万有引力定律一百多年以后，英国物理学家卡文迪许巧妙地利用扭秤装置，第一次在实验室里比较准确地测出了引力常量，引力常量的测出有着非常重要的意义，使得万有引力定律有了真正的实验价值．可以用测定地球表面物体重力加速度的方法，测定地球质量，因此卡文迪许被称为“能称出地球质量的人”．现测出引力常量G，地球表面物体重力加速度g，已知地球半径为R．求：
（1）地球的质量M；
（2）若发射一颗人造地球卫星，卫星的运行轨道距地面高度为h，该卫星的周期大小．

参考答案：（1）设地球表面上一物体的质量为m，
根据地球表面的物体受到的重力等于万有引力，有：
GMmR2=mg
解得：M=gR2G
（2）设人造地球卫星质量为m′，卫星在此轨道上做匀速圆周运动的周期为T，
根据万有引力提供向心力，有：
GMm/(R+h)2=m/(2πT)2(R+h)
所以T=2π

本题解析：

本题难度：一般

2、选择题  在圆轨道上运动的质量为m的人造地球卫星，它到地面的距离等于地球的半径R，地球表面上的重力加速度为g，则
A．卫星运动的速度为
B．卫星运动的周期为
C．卫星运动的加速度为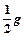
D．卫星的动能为

参考答案：BD

本题解析：略

本题难度：一般

3、选择题  如果该彗星被火星引力捕获后的轨道半径为R、周期为T，则由此可估算出火星的质量为（　　）
A．

参考答案：根据万有引力提供向心力GMmr2=m?4π2rT2，r=R，所以解得M=4π2R3GT2，
故选：C．

本题解析：

本题难度：简单

4、选择题  三颗人造地球卫星A、B、C处于不同的轨道上做匀速圆周运动，如图所示，下列说法正确的是（   ）

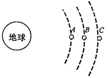
A．三颗卫星的线速度大小vA＜vB＜vC              
B．三颗卫星所受的地球引力的大小一定是FA＞FB＞FC
C．三颗卫星的向心加速度大小aA＞aB＞aC          
D．三颗卫星的运动周期TA＞TB＞TC

参考答案： C

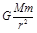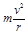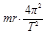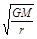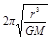本题解析：三颗人造地球卫星绕地球做圆周运动的的向心力均由地球对它们的万有引力提供，有：＝＝＝man，解得：v＝，T＝，an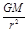＝，由图中关系可知rA＜rB＜rC，所以有：vA＞vB＞vC，aA＞aB＞aC，TA＜TB＜TC，故选项A、D错误；选项C正确；又由于卫星自身的质量不知，因此无法确定三颗卫星所受的地球引力大小的关系，故选项B错误。
考点：本题主要考查了万有引力定律、牛顿第二定律的应用问题。

本题难度：一般

5、选择题  下面所叙述的力，属于万有引力的是（　　）
A．马对车的拉力
B．地磁场对指南针的作用力
C．太阳对地球的吸引力
D．摩擦后的橡胶棒对小纸片的吸引力

参考答案：A、马拉车的力是弹力，不是万有引力，故A错误．
B、磁场对指南针的作用力是磁场力，不是万有引力，故B错误．
C、太阳对地球的吸引力是万有引力，故C正确．
D、地摩擦后的橡胶棒对小纸片的吸引力是静电力，不是万有引力，故D错误．
故选：B．

本题解析：

本题难度：简单