1、计算题 如图所示,倾角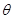 =30°。的光滑斜面MN底端固定一轻弹簧,轻弹簧的上端与滑块A固定连接,弹簧劲度系数k-100N/m,A静止且与距斜面顶端N点相距x=0.10m。另一小滑块B在N点以初速度
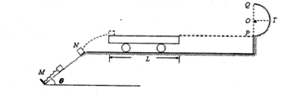
=30°。的光滑斜面MN底端固定一轻弹簧,轻弹簧的上端与滑块A固定连接,弹簧劲度系数k-100N/m,A静止且与距斜面顶端N点相距x=0.10m。另一小滑块B在N点以初速度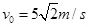 沿斜面向下运动,A、B碰撞后具有相同速度但不粘连。B与A分离后,B恰水平进入停放在光滑水平地面上的小车最左端,小车右端与墙壁足够远,小车上表面与半圆轨道最低点P的切线相平,小车与墙壁碰撞时即被粘在墙壁上。已知水平地面和半圆轨道面均光滑,滑块A、B可视为质点且质量均为m=2kg,被A压缩时弹簧存储的弹性势能Ep=0.5J,小车质量M=lkg、长L=l.0m,滑块B与小车上表面间的动摩擦因数
沿斜面向下运动,A、B碰撞后具有相同速度但不粘连。B与A分离后,B恰水平进入停放在光滑水平地面上的小车最左端,小车右端与墙壁足够远,小车上表面与半圆轨道最低点P的切线相平,小车与墙壁碰撞时即被粘在墙壁上。已知水平地面和半圆轨道面均光滑,滑块A、B可视为质点且质量均为m=2kg,被A压缩时弹簧存储的弹性势能Ep=0.5J,小车质量M=lkg、长L=l.0m,滑块B与小车上表面间的动摩擦因数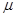 =0.2,g取l0m/s2。求:
=0.2,g取l0m/s2。求:
(I)滑块B与A碰撞结束瞬间的速度;
(2)小车与墙壁碰撞前瞬间的速度;
(3)为使滑块B能沿圆轨道运动而不脱离圆轨道,对轨道半径R有何要求?
参考答案:(1)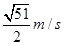 ;(2)
;(2)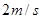 ;(3)
;(3)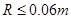 或
或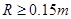
本题解析:(1)设碰撞前瞬间,B的速度为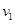 ,从释放B到与A撞前,由动能定理:
,从释放B到与A撞前,由动能定理:
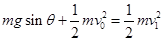
解得: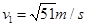
设撞后B的速度为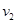 ,对B、A碰撞过程
,对B、A碰撞过程
由动量守恒定律可得: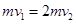
联立得: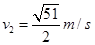 ? 5分
? 5分
(2)刚开始滑块A处于平衡状态,设此时弹簧压缩量为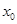 ,对A受力分析可得:
,对A受力分析可得:
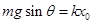
解得: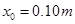
因 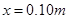
弹簧恢复原长时,上端的位置恰好在N点,B、A碰撞后,保持整体直至弹簧恢复原长时在N点分离。
设即将分离时A、B的速度为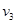 ,从A、B碰后开除以A、B即将分离,由动量守恒:
,从A、B碰后开除以A、B即将分离,由动量守恒:
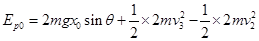
解得: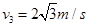
此后B从斜面飞出做斜抛运动直至最高点,设其落入小车最左端速度大小为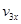 ,
,
则: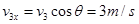
设小车的滑块共同速度为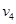 ,
,
滑块与小车相对运动过程中动量守恒: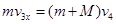
代入数据解得:
以滑块与小车的相对位移为L1,由动量守恒定律
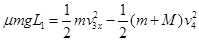
代入数据解得: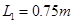
因小车左端距离墙壁足够远,则与墙壁碰撞前,滑块与小车具有共同的速度
故小车与墙壁碰撞时的速度 ? 10分
? 10分
(3)小车撞墙后,滑块将在小车上继续向右做匀速度为 ,
,
位移为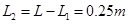 的匀减速运动,然后滑上圆轨道的最低点P。
的匀减速运动,然后滑上圆轨道的最低点P。
若滑块恰能滑上圆轨道的最高点Q,设此时的速度为v,
临界条件: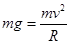
根据动能定理有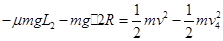
联立并代入数据得: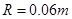
若滑块恰好滑至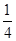 圆弧到达T点时速度减为0,则滑块也能沿圆弧轨道运动而不脱离轨道。
圆弧到达T点时速度减为0,则滑块也能沿圆弧轨道运动而不脱离轨道。
根据动能理: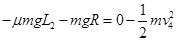
代入数据得: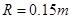
综上力述,滑块能沿圆轨道运动而不脱离圆轨道的半径
必须满足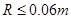 或
或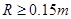 ? 5分
? 5分
本题难度:一般
2、选择题 在光滑水平面上有一木块保持静止,子弹穿过木块,下列说法中正确的是(? )
A.子弹对木块做功使木块内能增加
B.子弹损失的机械能等于子弹与木块增加的内能
C.子弹损失的机械能等于木块动能的增加和木块、子弹增加的内能的总和
D.子弹与木块总动能守恒
参考答案:AC
本题解析:子弹克服阻力做功等于产生的内能和木块的动能,所以木块的内能增加,故A正确;根据能量守恒得:子弹减少的机械能等于木块增加的机械能与系统增加的内能之和,B错误,C正确
子弹与木块组成的系统,总动量守恒,D错误
故选AC
点评:功是能量转化的量度,能量转化的多少可以用功来量度,掌握住功和能的关系就可以分析得出结论.
本题难度:简单
3、选择题 一带电小球在空中由a点运动到b点的过程中,受重力、电场力和空气阻力三个力作用.若重力势能增加3J,机械能增加0.5J,电场力做功1J,则小球( )
A.克服重力做功3?J
B.电势能增加1?J
C.克服空气阻力做功0.5?J
D.动能减少2.5?J
参考答案:A、重力做功等于重力势能的减小量,重力势能增加3J,故重力做功-3J,即克服重力做功3J,故A正确;
B、电场力做功等于电势能的减小量,电场力做功1J,故电势能减小1J,故B错误;
C、除重力外的各个力做的总功等于机械能的增加量,除重力外,只有电场力做功做功1J,而机械能增加0.5J、所以克服空气阻力做功0.5J,故C正确;
D、合力做功等于动能的增加量,合力做功等于各个分力做的功,总功为-2.5J,故动能减小2.5J,故D正确;
故选ACD.
本题解析:
本题难度:一般
4、选择题 质量为m的物体从静止出发以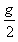 的加速度竖直下降h,下列说法中不正确的是
的加速度竖直下降h,下列说法中不正确的是
[? ]
A.物体的机械能增加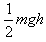
B.物体的机械能减少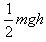
C.物体的动能增加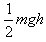
D.重力做功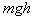
参考答案:A
本题解析:
本题难度:一般
5、选择题 如图所示,一个小物体在足够长的斜面上以一定初速度开始沿斜面向上运动,斜面各处粗糙程度相同,则物体以后在斜面上运动的过程中
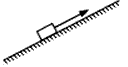
[? ]
A.动能一定一直减小
B.机械能一直减小
C.如果某段时间内摩擦力做功与物体动能的改变量相同,则此后物体动能将不断减小
D.如果某两段时间内摩擦力做功相同,则这两段时间内摩擦力做功功率一定相等
参考答案:B
本题解析:
本题难度:一般