1、选择题  如图所示，两段光滑圆弧轨道半径分别为R1和R2，圆心分别为O1和O2，所对应的圆心角均小于5°，在最低点O平滑连接。M点和N点分别位于O点左右两侧，距离MO小于NO。现分别将位于M点和N点的两个小球A和B（均可视为质点）同时由静止释放。关于两小球第一次相遇点的位置，下列判断正确的是

A．恰好在O点
B．一定在O点的左侧
C．一定在O点的右侧
D．条件不足，无法确定

参考答案：C

本题解析：如图所示为光滑圆弧轨道上的一小段，AB球的运动可以看做是单摆运动，根据单摆运动的周期公式即可求解．
AB球发生正碰后各自做单摆运动．，所以AB两球的周期不相同，由题目可知AB球下落到达O的时间为，两小球第一次相遇点的位置一定在O点的右侧?。
故选C．
点评：该题主要考查了单摆周期公式的直接应用，要注意周期与质量、速度等因素无关．

本题难度：一般

2、计算题  已知单摆摆长为L，悬点正下方3L/4处有一个钉子。让摆球做小角度摆动，其周期将是多大？

参考答案：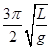

本题解析：摆长为L的单摆的周期为：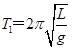
摆长为的单摆的周期为：
故小球完成一次全振动的时间为：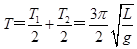

本题难度：简单

3、简答题  如图1-5所示，两根长度均为L的细线下端拴一质量为m的小球，两线间夹角为α,今使摆球在垂直纸面的平面内做小幅度振动，求其振动频率.

图1-5

参考答案：

本题解析：解题的关键是找到隐蔽的摆长.
这是一个双线摆，可以将其等效为一个单摆，求出等效摆长后，代入单摆周期公式，即得出所求.
此双线摆的等效摆长为L′=Lcos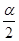，代入单摆周期公式即得所求周期：T=2π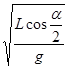,f==.

本题难度：简单

4、选择题  有一摆长为L的单摆，悬点正下方某处有一小钉，当摆球经过平衡位置向左摆动时，摆线的上部将被小钉挡住，使摆长发生变化，现使摆球做小幅度摆动，摆球从右边最高点M至左边最高点N运动过程的闪光照片，如图所示，(悬点和小钉未被摄入)，P为摆动中的最低点。已知每相邻两次闪光的时间间隔相等，由此可知，小钉与悬点的距离为

[? ]
A．L/4?
B．L/2?
C．3L/4?
D．无法确定

参考答案：C

本题解析：

本题难度：一般

5、选择题  将一个摆长为l的单摆放在一个光滑的，倾角为α的斜面上，其摆角为θ，如图．下列说法正确的是（　　）
A．摆球做简谐运动的回复力F=mgsinθsinα
B．摆球做简谐运动的回复力为mgsinθ
C．摆球做简谐运动的周期为2π

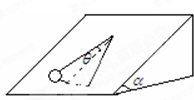
参考答案：A、B、本题是类似单摆模型，回复力是重力的下滑分力的切向分量提供，重力的下滑分力为mgsinα，下滑分力的切线分力为mgsinαsinθ，故A正确，B错误；
C、类似单摆模型，等效重力加速度为gsinα，故周期为：T=2π

本题解析：

本题难度：简单