1、简答题  因测试需要，一辆汽车在某雷达测速区，沿平直路面从静止开始匀加速一段时间后，又接着做匀减速运动直到最后停止．下表中给出了雷达测出的各个时刻对应的汽车速度数值．求：

参考答案：（1）由表给数据可分析：
前4?s内汽车做匀加速运动，加速度大小
a1=△v1△t1=6-32-1?m/s2=3?m/s2?
汽车做匀减速运动时的加速度
a2=△v2△t2=2-49-8?m/s2=-2?m/s2
大小为2?m/s2
（2）由表可知匀加速的最大速度是v=12?m/s?
根据运动学规律，匀加速的位移x1=v2-02a1=24?m?
同理可求得匀减速的位移x2=0-v22a2=36?m?
所以总位移x=x1+x2=60?m．
答：（1）汽车匀加速和匀减速两阶段的加速度a1、a2分别是3?m/s2?和-2?m/s2；（2）汽车在该区域行驶的总位移是60m．

本题解析：

本题难度：一般

2、简答题  初速度为零的匀加速直线运动的比例关系成立的条件是什么？对于末速度为零的匀减速直线运动可否应用这些比例关系？

参考答案：这些比例关系成立的条件是初速度为零的匀加速直线运动。对于末速度为零的匀减速直线运动，可以把它看成逆向的初速度为零的匀加速直线运动应用比例关系，这样可使问题简化，不过，关系中的第“1”、“第2” 就应该是倒数的“第1”、“第2”了。

本题解析：

本题难度：简单

3、选择题  一个物体做匀加速直线运动，它在第5s内的位移为9m，则下列说法正确的是（　　）
A．物体在第4.5秒末的速度一定是9m/s
B．物体的加速度一定是2m/s2
C．物体在前9s内的位移一定是81m
D．物体在第9s内的位移一定是17m

参考答案：由于匀加速直线运动的初速度未知，知道第5s内的位移，无法求出物体的加速度、前9s内内的位移，但是可以求出第5s内的平均速度，第5s内的平均速度为.v=xt=91m/s=9m/s，根据推论可知，物体在第4.5秒末的速度等于第5s内的平均速度，故第4.5秒末的速度一定是9m/s．故A正确，B、C、D错误．
故选A．

本题解析：

本题难度：一般

4、选择题  做匀加速直线运动的物体，下列说法正确的是（?）
A．在t秒内的位移决定于平均速度
B．第1秒内、第2秒内、第3秒内的位移之比是1：2：3
C．连续相等的时间间隔内的位移之差相等
D．初速度为0的匀变速直线运动连续相等位移的时间之比1：3：5

参考答案：AC

本题解析：由位移与平均速度的关系s=vt可知A对；对于初速度为零的匀加速直线运动第1秒内、第2秒内、第3秒内的位移之比是1:3:5，B错；在匀变速直线运动中连续相等的时间间隔内的位移之差相等，等于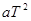，C对；初速度为0的匀变速直线运动连续相等位移的时间之比为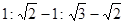
点评：对匀变速直线运动的推论要真正理解才能应用，应搞清楚每个运动推论应用的条件

本题难度：简单

5、简答题  电梯从静止开始加速上升，并从此时开始计时，其加速度随时间的变化如图所示：求：
（1）画出电梯的速度随时间的变化图象
（2）电梯在9s内发生的位移为多大．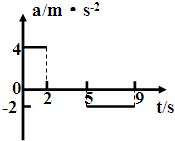

参考答案：（1）电梯先做加速度a=4m/s2的匀加速直线运动，2s末的速度v=at1=8m/s．然后做匀速直线运动．最后做加速度为-2m/s2的匀减速直线运动，9s末的速度v′=v+a′t′=8-2×4m/s=0m/s．


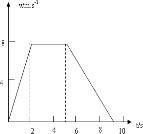
速度时间图线如图．
（2）在9s内位移x=12×(3+9)×8m=48m．
答：（1）速度时间图线如图．
（2）电梯在9s内发生的位移为48m．

本题解析：

本题难度：一般