1、选择题 据新闻报道:“嫦娥二号”探月卫星于2010年10月1日18时成功发射。卫星绕月运行的圆形轨道距月球表面约为100km,用118分钟绕月球运行一周,运行速度约1.6km/s。已知万有引力常量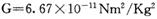 ,由以上信息可以估算下面哪些物理量
,由以上信息可以估算下面哪些物理量
A.月球半径?B月球的自转周期
C.“嫦娥二号”卫星的质量?D.月球表面重力加速度
参考答案:AD
本题解析:由公式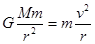 得
得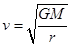 ,再根据公式
,再根据公式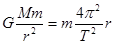 得
得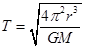 ,
,
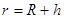 联立可得月球半径,A正确,根据题中的信息无法求出月球的自转周期,B错误
联立可得月球半径,A正确,根据题中的信息无法求出月球的自转周期,B错误
因为计算过程中卫星的质量消去了,所以也无法求出卫星的质量,C错误,
由公式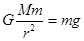 得
得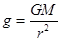 ,结合上述几个式子可得重力加速度,D正确
,结合上述几个式子可得重力加速度,D正确
故选AD
点评:应用万有引力定律进行卫星加速度、速度、周期和中心天体质量的估算
本题难度:一般
2、选择题 各行星绕太阳运行的轨道近似看做圆,若地球的轨道半径取为1.5×1011m,冥王星的轨道半径取为5.9×1012m,则冥王星的公转周期接近
A.4年
B.40年
C.150年
D.250年
参考答案:D
本题解析:由周期公式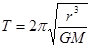 可知,冥王星的周期为地球周期的250倍,D对;
可知,冥王星的周期为地球周期的250倍,D对;
本题难度:简单
3、填空题 已知地球的半径为R,地面的重力加速度为g,引力常量为G?可求得地球的平均密度ρ=________。
参考答案:ρ="?" 3g/4πGR?。
本题解析:略
本题难度:简单
4、计算题 如图所示,离质量为M、半径为R、密度均匀的球体表面R远处有一质量为m的质点,此时M对m的万有引力为F1 ;当从M中挖去一半径为r=R的球体时,剩下部分对m的万有引力为F2,则F1与F2之比是多少?

参考答案:解:质点与大球球心相距2R,其万有引力为F1,则F1=
大球质量M=ρ×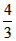 πR3,挖去的小球质量M′=ρ×
πR3,挖去的小球质量M′=ρ×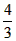 π(
π( )3 ,
)3 ,
即M′=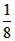 ρ×
ρ× πR3=
πR3=
小球球心与质点间相距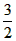 R,小球与质点间的万有引力为:F1′=
R,小球与质点间的万有引力为:F1′=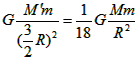
则剩余部分对质点m的万有引力为:F2=F1-F1′=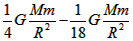 =
=
故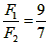 。
。
本题解析:
本题难度:困难
5、选择题 宇宙间存在一些离其它恒星较远的三星系统,其中有一种三星系统,如图所示,三颗质量均为m的星位于等边三角形的三个顶点,三角形边长为R,忽略其它星体对它们的引力作用,三星在同一平面内绕三角形中心O做匀速圆周运动,万有引力量为G,则
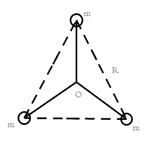
A.每颗星做圆周运动的线速度为
B.每颗星做圆周运动的角速度为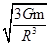
C.每颗星做圆周运动的周期为
D.每颗星做圆周运动的加速度与三星的质量无关
参考答案:ABC
本题解析:
每颗星受到的合力为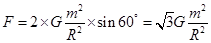 ,轨道半径为
,轨道半径为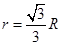 ,由向心力公式
,由向心力公式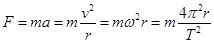 ,解得
,解得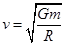 ,
,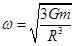 ,
,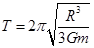 ,显然加速度a与m有关,故A、B、C均正确。.
,显然加速度a与m有关,故A、B、C均正确。.
本题难度:一般