1、选择题 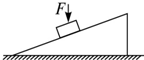 如图所示,放在固定斜面上的物块以加速度a沿斜面匀加速下滑,若在物块上再施加一个竖直向下的恒力F,则
如图所示,放在固定斜面上的物块以加速度a沿斜面匀加速下滑,若在物块上再施加一个竖直向下的恒力F,则
A.物块静止
B.物块仍以加速度a匀加速下滑
C.物块匀速下滑
D.以上说法都不对
参考答案:D
本题解析:分析:首先对物体不施加力F时受力分析,根据牛顿第二定律列出方程,然后再对物体施加力F时受力分析列出牛顿第二定律方程,比较可得出结论.
解答:当没施加力F时,物体受力分析如图所示,应有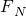 =mgcosθ,mgsinθ-
=mgcosθ,mgsinθ-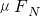 =ma,解得a=
=ma,解得a= =gsinθ-μgcosθ
=gsinθ-μgcosθ
施加力F后,应有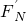 =(mg+F)cosθ,(mg+F)sinθ-
=(mg+F)cosθ,(mg+F)sinθ- =ma
=ma ,解得
,解得 =
=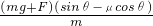 ,显然比较可知a′>a,所以ABC错误,应选D.
,显然比较可知a′>a,所以ABC错误,应选D.
故选D.
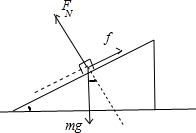
点评:解决动力学问题的关键是正确进行受力分析,然后根据牛顿第二定律列式求解即可.
本题难度:简单
2、计算题 (10分)已知月球的质量是地球质量的 ,月球半径是地球半径的
,月球半径是地球半径的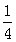 ,在月球表面16m处让质量m=50kg的物体自由下落,(已知地球表面的重力加速度g=10m/s2)。求:
,在月球表面16m处让质量m=50kg的物体自由下落,(已知地球表面的重力加速度g=10m/s2)。求:
(1)月球表面的重力加速度 是多大?
是多大?
(2)物体下落到月球表面所用的时间t是多少?
(3)月球的第一宇宙速度是地球的第一宇宙速度的多少倍?
参考答案:(1)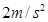 ;(2)4S;(3)
;(2)4S;(3)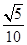
本题解析:(1)对星球表面上质量为 的物体:
的物体: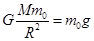 ? 2分
? 2分
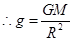 ?
? ?
?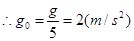 ?1分[
?1分[
(2)由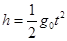 得:?2分
得:?2分
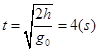 ?1分
?1分
(3)由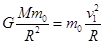 得:? 2分
得:? 2分
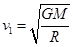 ?
?
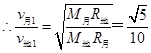 ? 1分
? 1分
本题难度:一般
3、填空题 已知地球同步卫星离地面的高度约为地球半径的6倍.若某行星的平均密度为地球平均密度的一半,它的同步卫星距其表面的高度是其半径的2.5倍,则该行星的自转周期约为______小时.
参考答案:地球的同步卫星的周期为T1=24小时,轨道半径为r1=7R1,密度ρ1.
某行星的同步卫星周期为T2,轨道半径为r2=3.5R2,密度ρ2.
根据牛顿第二定律和万有引力定律分别有:
Gm1ρ143πR31r21=m1r1(2πT1)2
Gm2ρ243πR32r22=m2r2(2πT2)2
两式化简解得:T2=T12=12 小时.
故答案为:12
本题解析:
本题难度:一般
4、选择题 A、B两颗地球卫星绕地球做圆周运动,运转的周期之比为 ,则
,则
A.轨道半径之比为
B.线速度之比为
C.向心加速度之比为
D.质量之比为
参考答案:B
本题解析:据题意,已知卫星的运转周期之比为 ,则轨道半径之比为:据
,则轨道半径之比为:据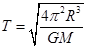 ,即
,即 ,故选项A错误;线速度之比为:据
,故选项A错误;线速度之比为:据 ,即
,即 ,故选项B正确;向心加速度之比为:据
,故选项B正确;向心加速度之比为:据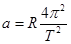 ,即
,即 ,故选项C错误;卫星的质量比无法计算,故选项D错误。
,故选项C错误;卫星的质量比无法计算,故选项D错误。
考点:本题考查万有引力定律。
本题难度:一般
5、选择题 两个绕太阳运行的行星质量分别为m1和m2,轨道半径分别为r1和r2,若它们只受太阳引力的作用,则这两个行星的向心加速度之比为
[? ]
A.1:1
B.m2r1:m1r2
C.m1r2:m2r1
D.r22:r12
参考答案:D
本题解析:
本题难度:一般