1、计算题  一辆汽车从静止开始做匀加速直线运动，加速度大小a=3m/s2，求经过10 s后汽车速度的大小？在这段时间里汽车运动了多远？

参考答案：s =" 150" m

本题解析：解：由匀变速直线运动公式得：v = at? (3分)
代入数据得：v =" 30" m / s?（2分）
s = 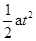?(3分)
代入数据得：s =" 150" m?（2分）
本题考查了匀变速直线运动，根据公式v = at，s = 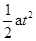可求解。

本题难度：简单

2、计算题  如图所示，质量为10kg的环在F=200N的拉力作用下，沿固定在地面上的粗糙长直杆由静止开始运动，杆与水平地面的夹角θ=37°，拉力F与杆的夹角为θ。力F作用0.5s后撤去，环在杆上继续上滑了0.4s后速度减为零。（已知sin37°=0.6,cos37°=0.8,g=10m/s2）求：

（1）环与杆之间的动摩擦因数μ；
（2）环沿杆向上运动的总距离s。

参考答案：（1）0.5 （2）1.8 m

本题解析：（1）设环做匀加速直线运动和匀减速直线运动的加速度大小分别为a1和a2，撤去力F瞬间物体的速度为v，则由?v=a1t1和?0=v-a2t2
得a1t1=a2t2?，代入数据得2a1=1.6a2?①
根据牛顿第二定律得
Fcosθ-mgsinθ-μ（Fsinθ-mgcosθ）=ma1?②
mgsinθ+μmgcosθ=ma2?③
由①②③式联立解得μ=0.5。
（2）将μ=0.5代入②③得a1=8m/s2，a2=10m/s2
所以环沿杆向上运动的总距离
s=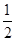a1t12+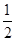a2t22=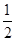（×8×0.52+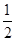×10×0.42）m=1.8m．

本题难度：一般

3、选择题  甲、乙两人同时由相同位置A沿直线运动到同一位置B，甲先以速度v1匀速运动了一半路程，然后以速度v2匀速走完剩下的后一半路程；乙在由A地运动到B地的过程中，前一半时间运动速度为v1，后一半时间的运动速度为v2，若v1< v2，则甲与乙比较，以下正确的是（?）
A．甲先到达B地
B．乙先到达B地
C．只要取值合适，甲、乙两人可以同时到达
D．以上情况都有可能

参考答案：B

本题解析：设AB两地相距x，则t甲＝＋，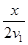
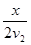所以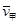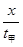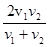＝＝，设乙从A→B经历时间为t，则
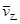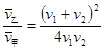＝，所以.由于
(v1＋v2)2－4v1v2＝(v1－v2)2＞0，所以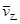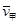＞，所以由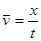得t乙＜t甲，即乙先到达B地，应选B.
点评：在比较谁先到达目的地的问题时，可比较两人到达目的地所用时间，把一个问题分成求解两个时间，使思路变得清晰

本题难度：一般

4、简答题  一辆汽车在十字路口等待绿灯．绿灯亮起时，它以3m/s2的加速度开始行驶，恰在此时，一辆自行车以6m/s的速度并肩驶出．试求：
（1）汽车追上自行车之前，两车之间的最大距离．
（2）何时汽车追上自行车？追上时汽车的速度多大？

参考答案：（1）汽车在追及自行车时，当他们经过时间t1速度相等时，两者相距最远△S．那么有
V汽=V自?
?即at1=V0t1=V0a=6m/s3m/s2=2s
△S=V0t1-12at12=6m/s×2s-12×3m/s2×(2s)2=6m
（2）设经过时间t2，汽车追上自行车，那么有；S1=12at22S2=v0t2
当S1=S2即?12at22=v0t2有?t2=2v0a=2×6m/s3m/s2=4s
此时，汽车的速度为?v2=at2=3m/s2×4m/s=12m/s
答：（1）汽车追上自行车之前，两车之间的最大距离为6m．
（2）经过4s汽车追上自行车，追上时汽车的速度为12m/s

本题解析：

本题难度：一般

5、选择题  某质点做匀变速直线运动，经历一段时间通过一段位移。质点在该时间段中间时刻的速度为v1；在位移的一半处（即中点）的速度为v2，则以下说法正确的是
[? ]
A．只有质点做匀加速运动时，才有v1<v2
B．只有质点做匀减速运动时，才有v1<v2
C．无论质点是匀加速还是匀减速总有v1<v2
D．无论质点是匀加速，还是匀减速总是v1>v2

参考答案：C

本题解析：

本题难度：一般