1、计算题 如图所示,固定在竖直平面内的光滑半圆形轨道与粗糙水平轨道在B点平滑连接,轨道半径R=0.5m,一质量m=0.2kg的小物块(可视为质点)放在水平轨道上的A点,A与B相距L=10m,物块与水平轨道间的动摩擦因数μ=0.1。现用一水平恒力F向右推物块,已知F=3N,当物块运动到C点时撤去该力,设C点到A点的距离为x。在圆轨道的最高点D处安装一压力传感器,当物块运动到D点时传感器就会显示相应的读数FN,压力传感器所能承受的最大压力为90N,g取10m/s2,空气阻力不计。
(1)要使物块能够安全通过圆轨道的最高点D,求x的范围;
(2)在满足(1)问的情况下,在坐标系中作出压力传感器的读数FN与x的关系图象。
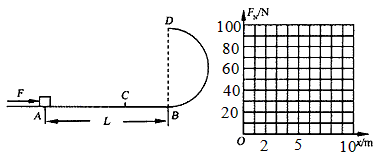
参考答案:解:(1)A到B过程,由得动能定理
B到D过程,由动能定理得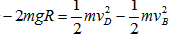
物块到达D点时,有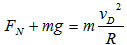
由以上三式得:
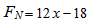 ,
,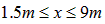
解得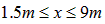 。
。
(2)
本题解析:
本题难度:一般
2、计算题 据报道,国际上已有科学家在研制一种可发射小型人造卫星的“超级大炮”.在“超级大炮”的许多气室中燃烧易燃气体,产生几乎是恒定的压力来推动卫星,它可以将一个体积约2m3、重4000N的卫星以3000m/s的速度发射出去,再用辅助火箭推进,最终将卫星送入轨道.发射的炮管长650m,与水平地面的夹角为30o,假设卫星被气体推动的横截面积为0.5m2,不计一切摩擦,求气体推力的平均压强.?
参考答案: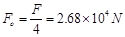
本题解析:解: 运用动能定理:
?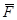 L-mgLsin30o=
L-mgLsin30o=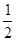 mv2-0? (6分)
mv2-0? (6分)
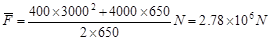 (2分)
(2分)
?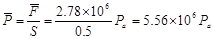 ?(2分)
?(2分)
运用牛顿定律同样给分:
?
 (3分)
(3分)
?
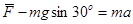 ?(3分)
?(3分)
?
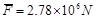 ?(2分)
?(2分)
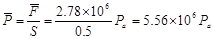 ?(2分)
?(2分)
?
本题难度:简单
3、简答题
(1)物体A在斜面上的运动情况?说明理由。
(2)物体A在斜面上运动过程中有多少能量转化为内能?(结果用字母表示)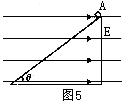
参考答案:(1)见解析
(2)
本题解析:(1)物体A在斜面上受重力、电场力、支持力和滑动摩擦力的作用,<1>小物体A在恒力作用下,先在斜面上做初速度为零的匀加速直线运动;<2>加上匀强磁场后,还受方向垂直斜面向上的洛伦兹力作用,方可使A离开斜面,故磁感应强度方向应垂直纸面向里。随着速度的增加,洛伦兹力增大,斜面的支持力减小,滑动摩擦力减小,物体继续做加速度增大的加速运动,直到斜面的支持力变为零,此后小物体A将离开地面。
(2)加磁场之前,物体A做匀加速运动,据牛顿运动定律有:

解出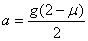
A沿斜面运动的距离为:

加上磁场后,受到洛伦兹力
随速度增大,支持力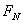 减小,直到
减小,直到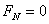 时,物体A将离开斜面,有:
时,物体A将离开斜面,有:
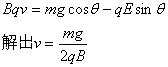
物体A在斜面上运动的全过程中,重力和电场力做正功,滑动摩擦力做负功,洛伦兹力不做功,根据动能定理有:
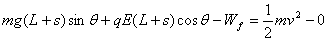
物体A克服摩擦力做功,机械能转化为内能:

本题难度:简单
4、选择题 如图所示,带电平行金属板A、B,板间的电势差为U,A板带正电,B板中央有一小孔.一带正电的微粒,带电量为q,质量为m,自孔的正上方距板高h处自由落下,若微粒恰能落至A、B两板的正中央c点,不计空气阻力,
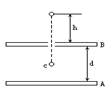
则:
A.微粒在下落过程中动能逐渐增加,重力势能逐渐减小
B.微粒在下落过程中重力做功为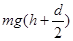 ,电场力做功为
,电场力做功为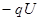
C.微粒落入电场中,电势能逐渐增大,其增加量为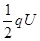
D.若微粒从距B板高1.5h处自由下落,则恰好能达到A板
参考答案:C
本题解析:微粒在下落过程中先做加速运动,后做减速运动,动能先增大,后减小.重力一直做正功,重力一直减小.故A错误.
微粒下降的高度为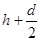 ,重力做正功,为
,重力做正功,为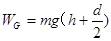 ,,电场力向上,位移向下,电场力做负功,
,,电场力向上,位移向下,电场力做负功,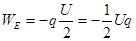 .故B错误.
.故B错误.
微粒落入电场中,电场力做负功,电势能逐渐增大,其增加量等于微粒克服电场力做功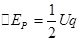 ,C正确,
,C正确,
由题微粒恰能落至A,B板的正中央c点过程,由动能定理得: 。若微粒从距B板高2h处自由下落,设达到A板的速度为v,则由动能定理得:
。若微粒从距B板高2h处自由下落,设达到A板的速度为v,则由动能定理得: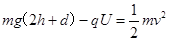 由①②联立得v=0,即恰好能达到A板.故D错误.
由①②联立得v=0,即恰好能达到A板.故D错误.
考点:
点评:题根据动能定理研究微粒能否到达A板,也可以根据牛顿第二定律和运动学公式分析.
本题难度:一般
5、填空题 质量为m =4kg的木块,在与水平成370大小为10N的水平恒力作用下,在光滑的水平面上由静止开始运动,运动时间t=5s,则力F在t=5s内对木块做功的平均功率为?W,5s末木块的动能为?J。
参考答案:40,200
本题解析:本题考查的是动能定理的问题,整个过程中仅有恒力做功,故做功大小等于末动能,
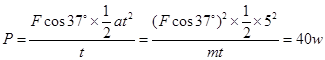 ,
,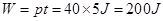
本题难度:一般