1、简答题  如图所示，两个完全相同、质量都是m的金属小球甲、乙套在光滑绝缘杆上，P左侧杆水平，且处于水平向左场强为E的匀强电场中，右侧是半径为尺的四分之一圆弧杆．甲球带电荷量为q的负电荷，乙球不带电并静止于M处，PM=L．现将甲球从圆弧杆顶端无初速?释放，运动到M时与乙碰撞并粘合在一起向左运动．碰撞时间极短，水平杆足够长．求：
（1）甲在碰撞前瞬间的速度大小．
（2）碰撞后甲乙共同向左运动的最大距离．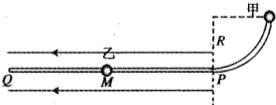

参考答案：（1）甲球在运动到M点的过程中，根据动能定理得
? mgR-qEL=12mv2-0
解得? v=

本题解析：

本题难度：一般

2、选择题  在光滑的地板上，用水平拉力分别使两个物块由静止获得相同的动能，那么可以肯定（?）
A．水平拉力相等
B．两物块质量相等
C．两物块速度变化相等
D．水平拉力对两物块做功相等

参考答案：D

本题解析：根据动能定理，物体所受的合外力就是拉力，拉力对物体做的功等于物体动能的增量，两个物体从静止开始获得的动能相同，一定是拉力做的功相同，D正确

本题难度：简单

3、简答题  某学校科技小组对一辆自制小遥控车的性能进行研究，他们让小车在水平地面上由静止开始运动，并将小车运动的全过程记录下来，通过数据处理得到如图所示的v-t图象，已知小车在0-2s内做匀加速直线运动，2-10s内小车牵引力的功率保持不变，在10s末停止遥控，关闭电动机．小车的质量m=1kg，整个过程中小车受到的阻力保持不变．求：
（1）小车所受的阻力f；
（2）小车在2-10s内牵引力的功率；
（3）小车在14s内阻力f做的功．

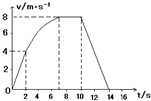
参考答案：（1）在7～10s内小车匀速运动故F=f，所以P=Fv=fvmax=8f，
而在0～2s内小车的加速度a=△v△t=42=2m/s2，
根据牛顿第二定律可知：F合=ma，
即F-f=ma，
所以：F=f+ma=f+1×2=f+2，
故在t=2s时有：P=（f+2）×4，
由于在2～10s内牵引力的功率保持不变，
所以f×8=（f+2）×4，
解得：f=2N．
（2）t=10s时牵引力的功率P=Fv=2×8=16W；
（3）摩擦力在0～2s内所做的功为：W1=-fx1=-2×4×22=-8J，
根据动能定理2～10s对小车有：P△t+W2=12mv2-12mv22，
解得：W2=-P△t+12mv2-12mv22=-16×8+12×1×（64-16）=-128+24=-104J，
在10～14s时间内小车做匀减速运动，其加速度a′=fm=-22=-1m/s2，
所以在t=14s时物体的速度v3=0，
故在10～14s内阻力对小车所做的功为：W3=-2×8+02×4=-32J，
故0～14s内摩擦阻力对小车所做的功为：W=W1+W2+W3=-8-104-32=-144J．
答：（1）小车所受的阻力为2N；（2）小车在2-10s内牵引力的功率为16W；（3）小车在14s内阻力f做的功为-144J．

本题解析：

本题难度：一般

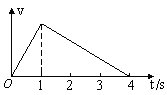
4、选择题  汽车从静止开始做匀加速直线运动，到最大速度时刻立即关闭发动机，滑行一段后停止，总共经历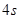，其速度—时间图象如图所示。若汽车所受牵引力为F，阻力为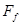，在这一过程中，汽车所受的牵引力做功为W1，阻力所做的功为W2，则

A．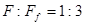
B．
C．
D．

参考答案：BD

本题解析：由动能定理可知，拉力做功与克服摩擦力做功大小相等，D对；在1s-4s间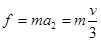,在加速度阶段，B对；

本题难度：简单

5、简答题  斜雪道的长为25m，顶端高为15m，下端经过一小段圆弧过渡后与很长的水平雪道相接，如图所示．一滑雪运动员在倾斜雪道的顶端以水平速度v0=8m/s飞出，在落到倾斜雪道上时，运动员靠改变姿势进行缓冲使自己只保留沿斜面的分速度而不弹起．除缓冲外运动员可视为质点，过渡轨道光滑，其长度可忽略．设滑雪板与雪道的动摩擦因数μ=0.2，求
（1）运动员落到倾斜雪道上时速度大小
（2）运动员在水平雪道上滑行的距离（取g=10m/s2）

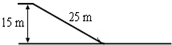
参考答案：（1）设平抛运动的水平分位移为x，竖直分位移为y，根据几何关系，有
y=x?tanθ=34x
运动员飞出后做平抛运动
x=v0t
y=12gt2
联立三式，得飞行时间：t=1.2 s
落点的x坐标：x1=v0t=9.6 m
落点离斜面顶端的距离：s1=12gt2sinθ=12m
落点距地面的高度：h1=（L-s1）sinθ=7.8m
接触斜面前的x分速度：vx=8m/s
y分速度：vy=gt=12m/s
沿斜面的速度大小为：vB=vxcosθ+vy sinθ=13.6m/s
即运动员落到倾斜雪道上时速度大小为13.6m/s．
（2）设运动员在水平雪道上运动的距离为s2，由功能关系得：
mgh1+12mvB2=μmgcosθ（l-s1）+μmgs2
解得：s2=74.8 m
即运动员在水平雪道上滑行的距离为74.8m．

本题解析：

本题难度：一般