1、选择题  下列哪一事件的发生使当事人被称为“能称出地球质量的人”（　　）
A．万有引力定律的发现
B．开普勒运动定律的发现
C．引力常量的测量
D．“以太”的提出

参考答案：C

本题解析：

本题难度：一般

2、计算题  2007年10月24日，我国“嫦娥一号”探月卫星成功发射。“嫦娥一号”卫星开始绕地球做椭圆轨道运动，经过变轨、制动后，成为一颗绕月球做圆轨道运动的卫星。设卫星距月球表面的高度为h，做匀速圆周运动的周期为T。已知月球半径为R，引力常量为G。求：
（1）月球的质量M；
（2）月球表面的重力加速度g；
（3）月球的密度。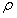

参考答案：解：（1）万有引力提供向心力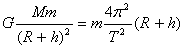
求出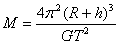
（2）月球表面万有引力等于重力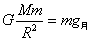
求出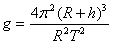
（3）根据，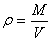
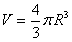
求出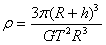

本题解析：

本题难度：一般

3、简答题  已知火星的半径为地球半径的一半,火星的质量为地球质量的1/9,已知一物体在地球上的重量比在火星上的重量大98N,求这个物体的质量是多少.(地球表面的重力加速度为g0=9.8m/s2)

参考答案：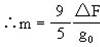

本题解析：设质量为m的物体在地球表面受到地球引力
　　　　　?
　　　质量为m的物体在火星表面受到火星的引力
　　　　　?
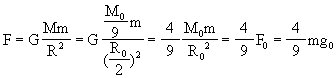　　　则此物体在地表和火表的重量差.
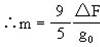　　　　　?　　　　　?m="18kg?"

本题难度：简单

4、选择题  地球表面的平均重力加速度为g，地球半径为R，万有引力常量为G，则可以用下列哪一式来估算地球的平均密度（　　）
A．

参考答案：根据地在地球表面万有引力等于重力有：
GMmR2=mg
解得：M=gR2G
所以ρ=MV=3g4πGR．
故选A．

本题解析：

本题难度：简单

5、选择题  2012年10月，美国耶鲁大学的研究人员发现一颗完全由钻石组成的星球，通过观测发现该星球的半径是地球的2倍，质量是地球的8倍，假设该星球有一颗近地卫星，下列说法正确的是（　　）
A．该星球的密度是地球密度的2倍
B．该星球表面的重力加速度是地球表面重力加速度的4倍
C．该星球的近地卫星周期跟地球的近地卫星周期相等
D．该星球近地卫星的速度是地球近地卫星速度的4倍

参考答案：解；A、根据V=43πR3可知，该星球的体积是地球体积的8倍，根据ρ=mV及质量是地球的8倍可知，该星球的密度与地球密度相同，故A错误；
B、根据GMmR2=mg得：g=GMR2，该星质量是地球的8倍，半径是地球的2倍，所以该星球表面的重力加速度是地球表面重力加速度的2倍，故B错误；
C、根据GMmR2=m4π2RT2解得；T=

本题解析：

本题难度：简单