1、选择题  “嫦娥一号”卫星发射后通过自带的小型火箭多次变轨，进入地月转移轨道，最终被月球引力捕获，成为绕月卫星，并开展对月球的探测。已知卫星绕月运动的周期约为127分钟，月球绕地球运动的轨道半径与卫星绕月球运动的轨道半径之比约为220。利用上述数据以及日常的天文知识，可估算出地球对卫星与月球对卫星的万有引力的比值约为（?）
A．2×10-3
B．0.2
C．7
D．2×102

参考答案：A

本题解析：我们先讨论地球与月球质量比例关系，月球绕地球运动周期大约为一月，则有
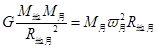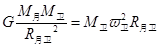，得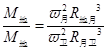
那么地球对卫星与月球对卫星的万有引力的比值约为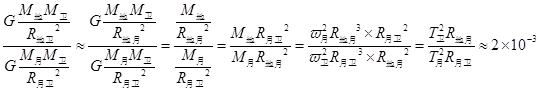，所以A正确。

本题难度：一般

2、选择题  已知引力常量G，则还需知道下面哪一选项中的数据，可以计算地球的质量？（　　）
A．已知地球绕太阳运行的周期及地球中心到太阳中心的距离
B．已知月球绕地球运行的周期及月球中心到地球中心的距离
C．已知人造地球卫星在地面附近绕行的速度
D．已知地球同步卫星离地面的高度

参考答案：
A、地球绕太阳做圆周运动，由太阳的万有引力提供向心力，则得：
GM日m地r2日地=m地4π2T2地r日地
则得：M日=4π2r3日地GT2地，可知能求出太阳的质量，不能求出地球的质量，故A错误．
B、同理，已知月球绕地球运行的周期及月球中心到地球中心的距离，能求出地球的质量，故B正确．
C、人造地球卫星在地面附近绕行时，由GMmR2=mv2R，则地球的质量 M=Rv2G，由于地球的半径R未知，不能求出地球的质量，故C错误．
D、对于地球同步卫星，由GMm(R+h)2=m4π2T2（R+h），则得地球的质量 M=4π2(R+h)3GT2，由于地球的半径R和自转周期T均未知，所以不能求出地球的质量．故D错误．
故选：B．

本题解析：

本题难度：简单

3、简答题  某行星与地球的质量比为a，半径比为b，该行星表面与地球表面的重力加速度比为______．

参考答案：根据万有引力等于重力GMmR2=mg得，g=GMR2，知重力加速度与中心天体的质量和半径有关，所以g1g2=ab2
故答案为：a：b2

本题解析：

本题难度：一般

4、选择题  下列说法符合史实的是（　　）
A．牛顿发现了行星的运动规律
B．开普勒发现了万有引力定律
C．哥白尼提出了“日心说”推翻了束缚人类思想很长时间的“地心说”
D．牛顿发现了海王星和冥王星

参考答案：Ｃ

本题解析：

本题难度：一般

5、简答题  中国“嫦娥一号”绕月探测卫星完成三次近月制动后，成功进入周期T=127min、高度h=200km的近月圆轨道．（保留两位有效数字）
已知月球半径为R=1.72×106?m，当卫星在高度h=200km的圆轨道上运行时：
①卫星的线速度υ=？
②该轨道处的重力加速度g′=？

参考答案：①嫦娥一号的线速度υ=2π(R+h)T=2×3.14×1.92×106127×60=1.6×103m/s；
②卫星做圆周运动的向心力由万有引力（重力）提供，由牛顿第二定律得：
m′g=m′v2R+h，
解得：g′=v2R+h=(1.6×103)21.92×106=1.3m/s2；
答：①卫星的线速度υ=1.6×103m/s；
②该轨道处的重力加速度g′=1.3m/s2．

本题解析：

本题难度：一般