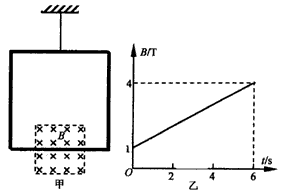
1、计算题  轻质细线吊着一质量为m=0.32 kg，边长为L=0.8 m、匝数n=10的正方形线圈，总电阻为r=1 Ω。边长为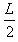的正方形磁场区域对称分布在线圈下边的两侧，如图甲所示，磁场方向垂直纸面向里，大小随时间变化规律如图乙所示，从t=0开始经t0时间细线开始松弛，g=10 m/s2。求：
(1)在前t0时间内线圈中产生的电动势；
(2)在前t0时间内线圈的电功率；
(3)求t0的值。

参考答案：解：(1)由法拉第电磁感应定律得：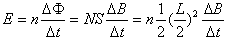
?(2)线圈中的电流为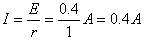
线圈的电功率为P=I2r=0.16 W
(3)分析线圈受力可知，当细线松弛时有：F安=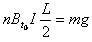


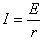
由图象知：Bt0=1+0.5t0
解得：t0=2 s

本题解析：

本题难度：困难

2、选择题  一矩形线框置于匀强磁场中，线框平面与磁场方向垂直先保持线框的面积不变，将磁感应强度在1s时间内均匀地增大到原来的两倍接着保持增大后的磁感应强度不变，在1s时间内，再将线框的面积均匀地减小到原来的一半，先后两个过程中，线框中感应电动势的比值为
[? ]
A.1/2
B.1
C.2
D.4

参考答案：B

本题解析：

本题难度：一般

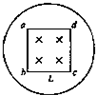
3、选择题  如图所示，半径为r的n匝圆形线圈套在边长为L的正方形abcd之外，匀强磁场仅在正方形区域内且垂直穿过正方形所在平面，当磁感应强度以

参考答案：由题意知，线圈磁通量的变化率△Φ△t=△B△tS=△B△t?L2；根据法拉第电磁感应定律得感应电动势大小为：
E=n△Φ△t=n△B△t?L2；
故选：D

本题解析：

本题难度：一般

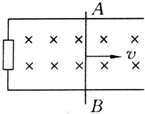
4、选择题  如图，导体AB在做切割磁感线运动时，将产生一个电动势，因而在电路中有电流通过，下列说法中正确的是（　　）
A．因导体运动而产生的感应电动势称为动生电动势
B．动生电动势的产生与洛仑兹力有关
C．动生电动势的产生与电场力有关
D．动生电动势和感生电动势产生的原因是一样的