1、填空题  如图所示，匀强磁场磁感应强度为B=0.2 T，方向垂直纸面向里，在磁场中的P点引入质量为m=2.0×108kg、带电荷量为q=5×10-6 C的正粒子，并使之以v=10 m/s的速度垂直于磁场方向开始运动，运动方向如图所示，不计粒子重力，磁场足够大，则粒子做匀速圆周运动的半径为_________m，周期为_________s；穿过粒子圆周平面内的磁通量为_________Wb。

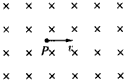
参考答案：0.2，0.04π（0.1256），0.008π（0.02512）

本题解析：

本题难度：一般

2、选择题  如图所示，竖直放置的两块很大的平行金属板a、b，相距为d，ab间的电场强度为E，今有一带正电的微粒从a板下边缘以初速度v0竖直向上射入电场，当它飞到b板时，速度大小不变，而方向变成水平方向，且刚好从高度也为d的狭缝穿过b板而进入bc区域，bc宽度也为d，所加电场大小为E，方向竖直向上，磁感应强度方向垂直于纸面向里，磁感应强度大小等于

参考答案：A、将粒子在电场中的运动沿水平和竖直方向正交分解，水平分运动为初速度为零的匀加速运动，竖直分运动为末速度为零的匀减速运动，根据运动学公式，有
水平方向：v0=at，d=v202g
竖直方向：0=v0-gt
解得
a=g? ①
t=v0t ②
故A正确；
B、粒子在复合场中运动时，由于电场力与重力平衡，故粒子做匀速圆周运动，洛伦兹力提供向心力
qv0B=mv2r
解得
r=mv0qB ③


由①②③得到r=2d，故B正确；
C、由于r=2d，画出轨迹，如图
由几何关系，得到回旋角度为30°，故在复合场中的运动时间为
t2=T12=πm6qB=πd3v0 故C错误；
D、粒子在电场中运动时间为
t1=d.vx=dv02=2dv0
故粒子在ab、bc区域中运动的总时间为t=t1+t2=(π+6)d3v0，故D正确；
故选ABD．

本题解析：

本题难度：一般

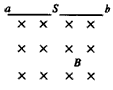
3、选择题  一个水平放置的挡板ab中间有一小孔S，一个质量为m、带电量为＋q的带电小球，从S处无初速度地进入一个足够大的匀强磁场中，磁场方向垂直纸碗里，磁感应强度大小为B，如图所示。小球最后将向右做匀速直线运动，则
[? ]

A．小球最后的速度为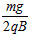
B．小球最后与ab的距离为
C．磁场对小球共做功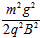
D．以上说法都不对

参考答案：B

本题解析：

本题难度：一般

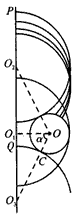
4、计算题  如图所示，匀强磁场的磁感应强度为B，方向垂直于纸面向里，MN为其左边界。磁场中有一半径为R、轴线与磁场平行的金属圆筒，圆筒的圆心O到MN的距离OO1=3R，OO1所在直线与圆筒右侧壁交于A点，圆筒通过导线与电阻r0，连接并接地。现有范围足够大的平行电子束以相同的速度从很远处垂直于MN向右射入磁场区。当金属圆筒最初不带电时，发现电子只能射到圆筒上以A点和C点为界的弧ADC上，而AEC弧上各点均不能接收到电子；当圆筒上电荷量达到相对稳定后，通过电阻r0的电流恒为I。已知电子质量为m，电荷量为e，忽略运动电子间的相互作用，取大地或无穷远处电势为零。求：
（1）在最初圆筒上没有带电时，电子射入磁场时的初速度v0；
（2）电阻r0中的电流恒定时电阻r0上端处的电势φ；
（3）电阻r0中的电流恒定时电子到达圆筒时速度v的大小和金属圆筒的发热功率P。

参考答案：解：（1）根据题意，电子在磁场中运动的轨道半径必定是r=4R，如图所示

由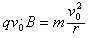，得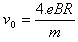
（2）稳定时，圆柱体上电荷不再增加，电阻r0两端电压为U，U=Ir0
电势φ=-Ir0
（3）电子从很远处射到圆柱表面时速度v满足
得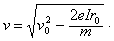
电流为I，单位时间到达圆筒的电子数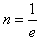
电子所具有总能量
消耗在电阻上的功率Pr=I2r0
所以圆筒发热功率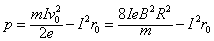

本题解析：

本题难度：困难

5、计算题  如图所示，条形区域AA"BB"中存在方向垂直于纸面向外的匀强磁场，磁感应强度B的大小为0.3 T，AA"，BB"为磁场边界，它们相互平行，条形区域的长度足够长，宽度d=1 m。一束带正电的某种粒子从AA"上的O点以沿着与AA"成60°角、大小不同的速度射入磁场，当粒子的速度小于某一值v0时，粒子在磁场区域内的运动时间t0=4×10-6 s；当粒子速度为v1时，刚好垂直边界BB"射出磁场，取π≈3，不计粒子所受重力，求：
(1)粒子的比荷。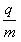
(2)速度v0和v1的大小。

参考答案：解：(1)若粒子的速度小于某一值v0时，则粒子不能从BB"离开磁场区域，只能从AA"边离开，无论粒子速度大小，在磁场中运动的时间相同，轨迹如图所示（图中只画了一个粒子的轨迹）

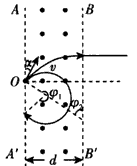
粒子在磁场区域内做圆周运动的圆心角均为φ1=240°
运动时间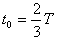
又
解得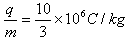或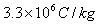
(2)当粒子速度为v0时，粒子在磁场内的运动轨迹刚好与BB"边界相切，此时有R0+R0sin30°=d
又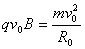
得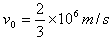
当粒子速度为v1时，刚好垂直边界BB"射出磁场区域，此时轨迹所对圆心角φ2=30°，有R1sin30°=d
又
得v1=2×106m/s

本题解析：

本题难度：困难