1、填空题  在方向水平的匀强电场中，一不可伸长的绝缘细线的一端连着一个质量为m的带电小球，另一端固定于O点．把小球拉起直至细线与场强平行，然后无初速度释放．已知小球摆到最低点的另一侧，线与竖直方向的最大夹角为θ．则小球电性为______（填正电或负电），经过最低点时细线对小球的拉力为______．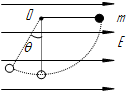

参考答案：依题，小球无初速度释放后做圆周运动，则小球带正电，否则小球做直线运动．
设细线长度为L．根据动能定理得
小球从释放到最低点的过程：mgL-qEL=12mv2? ①
小球无初速度释放摆到最低点的另一侧的过程：mgLcosθ-qEL（1+sinθ）=0? ②
小球最低点时
根据牛顿第二定律得
? F-mg=mv2L? ③
联立以上三式得
? F=mg(3-2cosθ)1+sinθ
故答案为：mg(3-2cosθ)1+sinθ

本题解析：

本题难度：一般

2、填空题  固定在水平地面上的光滑半球形曲面，半径为R，已知重力加速度为g．一小滑块从顶端静止开始沿曲面滑下，滑块脱离球面时的向心加速度大小为______，角速度大小为______．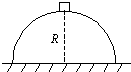

参考答案：设小球运动的竖直距离为h时，刚好脱离曲面，则有：
mgR-hR=mv2R①
由动能定理得：
12mv2=mgh②
由①②解得：v2R=23g
根据ω=vR得：
ω=

本题解析：

本题难度：一般

3、简答题  如图所示，一长度为R的轻质细绳与质量为m的小球相连，悬挂于O点．现将小球从水平位置P点自由释放．求：
（1）当细绳摆到竖直位置时小球的速度大小；
（2）当细绳摆到竖直位置时此时小球所受拉力的大小．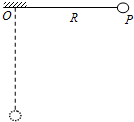

参考答案：（1）小球下摆的过程中，机械能守恒，
mgR=12mv2
得：v=

本题解析：

本题难度：一般

4、简答题  如图所示，在水平面直线MN的上方有一方向与MN成30°角的斜向右下方的匀强电场，电场区域足够宽，场强大小为E．在MN下方有一半径为R的圆形区域，圆心为O，圆O与MN相切于D点，圆形区域内分布有垂直纸面向里的匀强磁场．在MN上有一点C，圆心O与C点的连线和电场线平行，在OC的延长线上有一点P，P点到边界MN的垂直距离为0.5R．一质量为m、电荷量为q的带正电的粒子从P点静止释放．已知圆形磁场的磁感应强度大小为

2mE qR ，不计粒子的重力．求： （1）粒子在磁场中的运动半径r； （2）粒子最终离开电场时的速度v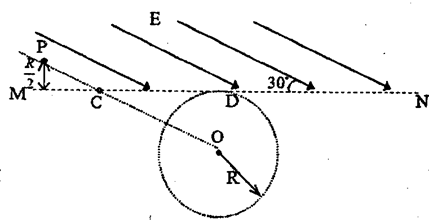． 参考答案：解（1）设粒子从C点射电场时速度为 由动能定理?qER2sin30°=12mV21 ∴V1= 本题解析： 本题难度：一般 5、简答题  有一竖直放置的圆形轨道，半径为R，由左右两部分组成，如图所示，右半部分AEB是光滑的，左半部分BFA是粗糙的，现在轨道最低点A放一个质量m的小球，并给小球一个水平向右的初速度v0，使小球沿轨道恰好运动到最高点B，且又能沿BFA轨道回到A点，小球回到A点时轨道的压力为4mg． 在求小球由BFA回到A点的速度vA时，甲同学的解法是：由于回到A点时对轨道的压力为4mg，故4mg=m vA2 R ，得vA=2 gR 在求小球在A点的初速度v0时，乙同学的解法是：由于小球恰好到达B点，故小球在B点的速度为零，则有： 1 2 mv02=2mgR，得v0=2 gR 试按以下要求作答： （1）你认为甲、乙两同学的解法是否正确？若不正确，请给出正确解法． （2）在小球由B点沿BFA轨道返回A点的过程中，求小球克服摩擦力做的功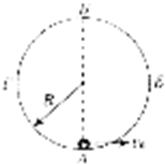． 参考答案：（1）甲同学的解法不正确 正确解法： 由于小球回到A点时轨道压力为4mg，则有： 4mg-mg=mvA2R?① 得vA= 本题解析： 本题难度：一般