1、简答题  汽车以10m/s的速度沿平直公路行驶，遇障碍物刹车后获得大小为a=5m/s2的加速度，假定汽车做匀减速直线运动求：
（1）刹车后3s内，汽车通过的位移大小
（2）第3s末汽车的速度大小．

参考答案：汽车刹车后做匀减速直线运动，设刹车时间为t0，则
t0=△v△t=0-10-5=2s＜3s
所以汽车2s末就已经停止运动，则第3s末汽车的速度大小v=0，
刹车后3s内，汽车通过的位移等于2s内通过的位移，则x=v0t+12at2=10×2-12×5×4=10m
答：（1）刹车后3s内，汽车通过的位移大小为10m；
（2）第3s末汽车的速度大小为0．

本题解析：

本题难度：一般

2、选择题  如图所示，一足够长的木板在光滑的水平面上以速度v匀速运动，现将质量为m的小物块对准木板的前端轻放，要使木板的运动速度保持不变，在物体开始接触木板到它与木板相对静止的过程中，需要对木板施加水平向右的力F，那么，在此过程中力F做功的数值为(已知物体与木板之间的动摩擦因数为μ)(? )

A．
B．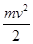
C．mv2
D．2mv2

参考答案：C

本题解析：小物块在木板上滑动的过程中，受重力mg、木板的支持力N和滑动摩擦力f作用，做匀加速直线运动，由于木板足够长，因此最终物块与木板具有相同的速度v，一起匀速运动，往后将不再需要力F作用于木板，设物块加速运动的位移为s1，时间为t，在此过程中，木板运动的位移为s2，根据匀变速直线运动规律和匀速直线运动规律有：s1＝，s2＝vt，根据滑动摩擦定律可知：f＝μmg，根据动能定理有：fs1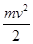＝－0，由功的定义式可知，力F做的功为：WF＝Fs2，由于开始时木板做匀速运动，因此，根据共点力平衡条件有：F＝f，联立以上各式解得：WF＝mv2，故选项C正确。

本题难度：一般

3、简答题  质量为m=4kg的物体与水平地面间的滑动摩擦因数为μ=0.2，现在F=20N的水平拉力作用下由静止开始在水平面内做匀加速直线运动，g=10m/s2?求：
（1）前2S内F对物体所做的功？
（2）2S末物体的动能？
（3）若2S末撤去F，则物体还可以向前运动多远？

参考答案：
（1）前2s内物体的加速度为a=F-μmgm=20-0.2×4×104m/s2=3m/s2
前2S内物体的位移为S=12at2=12×3×22m=6m
F对物体所做的功W=FS=20×6J=120J
（2）2s末物体的速度为v=at=6m/s，物体的动能为Ek=12mv2=12×4×62J=72J
（3）由动能定理得
-μmgS′=0-Ek
代入解得到S′=9m．
答：
（1）前2S内F对物体所做的功是120J．
（2）2S末物体的动能是72J．
（3）若2S末撤去F，物体还可以向前运动9m．

本题解析：

本题难度：一般

4、简答题  如图所示，一质量为M=4kg，长为L=1.5m的木板放在水平地面上，已知木板与地面间动摩擦因数为0.1，在此木板的右端上还有一质量为m=1kg的铁块，且视小铁块为质点，木板厚度不计；今对木板突然施加一个水平向右的拉力．?
①若不计铁块与木板间的摩擦，且拉力为8N，则小铁块经多长时间将离开木板？
②若铁块与木板间的动摩擦因数为0.2，铁块与地面间的动摩擦因数为0.1，要想小铁块对地的总位移不超过1.5m，则施加在木板水平向右的拉力满足什么条件？（g=10m/s2）

参考答案：（1）对长木板受力分析?有
F1=F-（M+m）gμ?
?a1=F1m=0.75m/s2?
? x1=L=12at2?
得t=2s
答：小铁块经2s将离开木板．
（2）相对地面：铁块在木版上时a1=μ1g=2m/s2；铁块在地面上时a2=μ2g=1m/s2；
木板对地面加速度a=F-f1-f2M，
f1=μ1gm，f2=μ2g（m+M）．
铁块相对地面位移有?2?a1x1=v12和2?a2x2=v12?并且满足?x2+x1≤1.5m．
令铁块在木版上滑行时间为t1，则v1=a1t1，则铁块对地面位移x1=12a1t12?和木板对地面位移?x=12at12，而且x=x1+L．
所以?F≥39N
答：施加在木板水平向右的拉力满足F≥39N．

本题解析：

本题难度：一般

5、填空题  甲、乙两物体从同一地点出发、沿同一方向做直线运动的速度--时间图象如图所示．若速度轴正方向为向南，则从第l?s末到第4s末乙的位移大小是______m；第4s末乙的加速度方向为______．在0-6s内，两物体最大距离是______m，两物体第二次相遇时甲的位移大小为______m．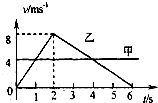

参考答案：从第l s末到第4s末乙的位移大小x=3×4+3×42=18m．第4s末乙正在做匀减速直线运动，加速度与速度反向，速度为正值，向南运动，则加速度的方向为向北．
从图上可以看成，第4s末两者相距最大，此时甲的位移x1=4×4m=16m，乙的位移x2=2×82+(4+8)×22m=20m，最大距离x′=20-16m=4m．
相遇时两者位移相等，知第6s两物体第二次相遇，则相遇时甲的位移大小x甲=6×4m=24m．
故答案为：18，向北，4，24．

本题解析：

本题难度：一般