1、填空题  某均匀介质中，两列简谐横波A和B同时沿x轴正方向传播，t=0时的波形如图所示，此时刻两列波的波峰正好在x=0处重合，该两列波的频率之比fA/fB=______，该时刻两列波的波峰另一重合处到x=0处的最短距离是______m．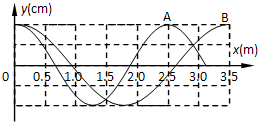

参考答案：由v=λf得：当波速一定时，波长与频率成反比．由图可知：λA：λB=2.5：3.5=5：7，所以fA：fB=7：5．
在该时刻波的波峰正好在x=0处重合，波峰另一重合处到x=0处的距离，由距离相等得：2.5×N=3.5×M，则N、M均取整数．若是最短距离，所以N=7，M=5．故最短距离为17.5m．
故答案为：75；17.5

本题解析：

本题难度：一般

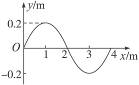
2、简答题  如图12-2-13所示，甲为某一波动在t="1.0" s时的图象，乙为参与该波动P质点的振动图象.

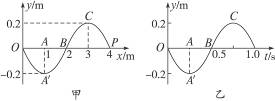
图12-2-13
（1）说出两图中AA′的意义.
（2）说出甲图中OA′B图线的意义.
（3）求该波速v.
（4）在甲图中画出再经3.5 s时的波形图.
（5）求再经过3.5 s时P质点的路程s和位移.

参考答案：（1）甲图中的AA′表示A质点的振幅，乙图中的AA′表示质点P的振幅.
（2）甲图中OA′B图线表示O到B之间所有质点在1.0 s时的位移情况.
（3）4 m/s
（4）如解析图所示
（5）2.8 m零

本题解析：（1）甲图中AA′表示A质点的振幅或1.0 s时x="1.0" m的质点的位移大小为0.2 m，方向为负；乙图中AA′表示P质点的振幅，也代表P质点在0.25 s内的位移大小为0.2 m,方向为负.
（2）甲图中OA′B段图线表示O到B之间所有质点在1.0 s时的位移，方向均为负.由乙图看出P质点在1.0 s时向-y方向振动，所以甲图中波向左传播，则OA′间各质点正向远离平衡位置方向振动，A′B间各质点正向靠近平衡位置方向振动.
（3）由甲图得波长λ="4" m,由乙图得周期T="1" s
所以波速v=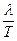="4" m/s.
（4）传播距离：Δx="v·Δt=4×3.5" m="14" m=(3+1/2)λ
所以只需将波形向x轴负向平移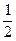λ="2" m即可，如下图所示.

（5）求路程：因为n=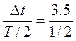=7
所以路程s="2An=2×0.2×7" m="2.8" m
求位移：由于波动的重复性，经历时间为周期的整数倍时，位移不变，所以只需考查从图示时刻P质点经T/2时的位移即可，所以经3.5 s质点P的位移仍为零.

本题难度：简单

3、填空题  如图所示，实线是一列简谐横波在t1 = 0时的波形图，虚线为t2=0.5s时的波形图，已知0＜t2－t1＜T， t1 = 0时，=2m处的质点A正向y轴正方向振动。则波的周期为?s； 波速大小为?m/s。

参考答案：2 s? 2m/s

本题解析：
试题分析: 根据t1=0时的波形图上=2m处的质点A正向y轴正方向振动，判断出波的传播方向沿着轴的正方向，已知0＜t2-t1＜T，则根据波形的平移得知，波传播的时间t2-t1=T/4得到T=4（t2-t1）=4×0.5s=2s．图知，波长λ=4m，则波速v=λ/T=2m/s．

本题难度：简单

4、选择题  （9分）P、Q是一列沿x轴传播的简谐横波中的两质点，水平间距为x＝20cm，从某时刻开始计时，两质点的振动图象如图所示，则：

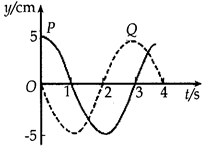
（i）根据图象，请写出做简谐振动的质点Q的位移（y）与时间（t）的函数关系式；
（ii）如果Q点比P点距离波源近，且P与Q之间水平距离大于1个波长，小于2个波长，求该简谐横波的传播速度v。

参考答案：（i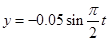）?（ii）?

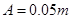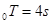本题解析：（i）从振动图可知，振幅，周期，结合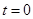时Q在平衡位置向下振动
对质点Q：
（ii）根据振动图像，P和Q振动步调相差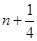周期，那么
根据P和Q之间水平距离大于1个波长，小于2个波长可知
带入计算得波长
传播速度

本题难度：一般

5、选择题  【选修3-4选做题】
两列简谐横波的振幅都是20cm，传播速度大小相同。实线波的频率为2Hz，沿x轴正方向传播；虚线波沿x轴负方向传播。某时刻两列波在如图所示区域相遇，则

[? ]
A.两列波在相遇区域会发生干涉现象
B.平衡位置为x＝6m处的质点此刻速度为零
C.平衡位置为x＝8.5m处的质点此刻位移y＞20cm
D.从图示时刻起再经过0.25s，平衡位置为x＝5m处的质点的位移y＞0

参考答案：C

本题解析：

本题难度：一般