1、选择题  欢庆节日的时候人们会在夜晚燃放焰火。某种型号的礼花弹从炮筒中射出后，4s末上升到离地面100m的最高点处，并恰好在此时炸开，构成美丽的图案。假设礼花弹从炮筒中竖直射出时的初速度是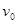，上升过程中所受的空气阻力大小始终是重力的k倍，那么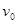和k分别等于（?）
A．25m/s，1.25
B．25m/s，0.25
C．50m/s，0.25
D．50m/s，1.25

参考答案：C

本题解析：上升过程中所受的平均阻力f=kmg，
根据牛顿第二定律得：a=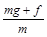=（k+1）g，
根据h=at2
得：a=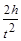=12.5m/s2，
所以v0=at=50m/s，
而（k+1）g=12.5m/s2，
所以?k=0.25．
故选C．

本题难度：一般

2、填空题  气球以v=4m/s的速度竖直匀速上升，其下方悬挂一重物，在气球上升到离地某一高度时悬绳突然断开，则此时重物的速度是______m/s，若重物经7秒钟落地，则悬绳断开时重物离地高为______m．

参考答案：重物离开气球时具有惯性，初速度为4m/s．
规定向下为正方向，则x=-v0t+12gt2=-4×7+12×10×49m=217m．
故答案为：4，217．

本题解析：

本题难度：一般

3、填空题  如果以速度v0将小球从地面竖直上抛，抛出时计时，那么小球速率变为 v0/2时与v0/4时物体距地面的高度比为____________.

参考答案：4/5

本题解析：设向上为正方向，根据竖直上抛物体的运动规律有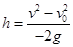，则，，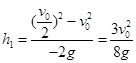
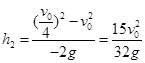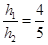
点评：中等难度。竖直上抛运动速度减小到零以前的运动可以看成是初速度为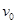，加速度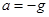的匀变速直线运动。

本题难度：简单

4、简答题  龙鱼（鱼类的一种）可以跳出水面捕食，在一次捕食过程中，龙鱼发现一只昆虫从其正上方2m高的树叶上滑落，与此同时龙鱼以4m/s的速度上跳，经过时间t捕捉到这只昆虫．试回答以下问题（g=10m/s2）
（1）时间t为多少？
（2）捕捉到昆虫时，龙鱼的速度？
（3）捕捉到昆虫时，龙鱼处于上升阶段还是下降阶段？此时距离水面多高？

参考答案：（1）龙鱼做竖直上抛运动，h1=v0t-12gt2 ①
昆虫做自由落体运动，h2=12gt2 ②
又：h1+h2=h ③
联立①②③，代入数据解得：t=0.5s
（2）捕捉到昆虫时，龙鱼的速度：v=v0-gt=4-10×0.5=-1m/s
负号表示运动的方向与初速度的方向相反，是向下．
（3）龙鱼的高度：h1=4×0.5m-12×10×0．52m=1.75m
答：（1）时间t为0.5s；（2）捕捉到昆虫时，龙鱼的速度大小是1m/s，方向向下；（3）捕捉到昆虫时，龙鱼处于下降阶段，此时距离水面高1.75m．

本题解析：

本题难度：一般

5、计算题  如图所示是建筑工地常用的一种“深穴打夯机”。工作时，电动机带动两个紧压夯杆的滚轮匀速转动将夯从深为h的坑中提上来，当两个滚轮彼此分开时，夯杆被释放，最后夯在自身重力作用下，落回深坑，夯实坑底。然后，两个滚轮再次压紧，夯杆再次被提上来，如此周而复始工作。已知两个滚轮边缘线速度v恒为4 m/s，每个滚轮对夯杆的正压力FN为2×104N，滚轮与夯杆间的动摩擦因数为0.3，夯杆质量m为1×103 kg，坑深h为6m。假定在打夯的过程中坑的深度变化不大，且夯杆底端升到坑口时，速度正好为零，取g=10m/s2，求：
(1)每个打夯周期中，电动机对夯杆所做的功；
(2)夯杆上升过程中被滚轮释放时夯杆底端离坑底多高；
(3)打夯周期。

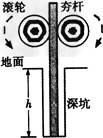
参考答案：解：(1)因为夯杆底端升到坑口时，速度正好为零，所以每个打夯周期中，电动机对夯杆所做的功W=mgh=6×104 J?
(2)根据题意，考虑到夯杆先匀加速上升，后匀速上升，再竖直上抛
当夯杆以v=4 m/s的初速度竖直上抛，上升高度为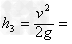：0.8 m
此时夯杆底端离坑底△h=h-h3=5.2 m
(3)以夯杆为研究对象f1=2μN=1.2×104 N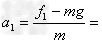；2m/s2
当夯杆与滚轮相对静止时：v=a1t1=4m/s，t1=2s，h1=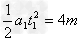
则当夯杆加速向上运动速度达到v=4 m/s后，夯杆匀速上升，匀速上升高度为：h2=h-h1-h3=1.2m
因此，夯杆上抛运动的时间为：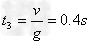
夯杆匀速上升的时间为：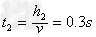
夯杆自由落体的时间为：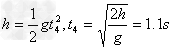
故打夯周期为：T=t1+t2+t3+t4=3.8 s

本题解析：

本题难度：困难