1、简答题  宇航员在某星球表面距地面4m高处自由释放一小球，经2秒落地．
（1）求该星球表面附近的重力加速度g1；
（2）已知该星球的半径与地球半径之比为R1：R2=1：4，求该星球的质量与地球质量之比M1：M2．（取地球表面重力加速度g2=10m/s2，空气阻力不计）
（3）若地球的第一宇宙速度约为8km/s，则此星球的第一宇宙速度为多大？

参考答案：（1）在某星球表面距地面4m高处自由释放一小球，经2秒落地，
根据自由落体运动规律得：h=12gt2
g1=2ht2=2m/s2．
（2）忽略星球自转的影响，根据万有引力等于重力列出等式
GMmR2=mg
M=gR2G
所以M1：M2=1：80?
（3）第一宇宙速度的表达式v=

本题解析：

本题难度：一般

2、简答题  月球自转一周的时间与月球绕地球运行一周的时间相等，都为T0．我国的“嫦娥1号”探月卫星于2007年11月7日成功进入绕月运行的“极月圆轨道”，这一圆形轨道通过月球两极上空，距月面的高度为h．若月球质量为M，月球半径为R，万有引力恒量为G．
（1）求“嫦娥1号”绕月运行的周期．
（2）在月球自转一周的过程中，“嫦娥1号”将绕月运行多少圈？
（3）“嫦娥1号”携带了一台CCD摄相机（摄相机拍摄不受光照影响），随着卫星的飞行，摄像机将对月球表面进行连续拍摄．要求在月球自转一周的时间内，将月面各处全部拍摄下来，摄像机拍摄时拍摄到的月球表面宽度至少是多少？

参考答案：（1）“嫦娥1号”轨道半径r=R+h，
? GmMr2=m4π2T2?r?
? 可得“嫦娥1号”卫星绕月周期T=2π

本题解析：

本题难度：一般

3、选择题  我国载人飞船“神舟七号”的顺利飞天，极大地振奋了民族精神.“神七”在轨道飞行过程中，宇航员翟志钢跨出飞船，实现了“太空行走”，当他出舱后相对于飞船静止不动时，以下说法正确的是（?）
A．他处于平衡状态
B．他不受任何力的作用
C．他的加速度不为零
D．他的加速度恒定不变

参考答案：C

本题解析：分析：翟志钢出舱后相对于飞船静止不动，与飞船一起绕地球做圆周运动，处于非平衡状态．他受到地球的万有引力，加速度不是零，而且加速度是变化的．
解答：解：A、翟志钢出舱后相对于飞船静止不动，与飞船一起绕地球做圆周运动，处于非平衡状态．故A错误．
B、翟志钢出舱后仍受到地球的万有引力．故B错误．
C、翟志钢出舱后与飞船一起绕地球做圆周运动，加速度不是零．故C正确．
D、翟志钢的加速度方向时刻在变化，加速度是变化的．故D错误．
故选C
点评：本题是实际问题，考查运用物理分析实际问题的能力．要抓住翟志钢做圆周运动，具有圆周运动的特点，如速度、加速度是变化的，受到向心力等等．

本题难度：简单

4、选择题  为了估算一个天体的质量需要知道绕该天体做匀速圆周运动的另一星球的条件是（引力常量G为已知）：①运转周期和轨道半径②质量和运转周期③轨道半径和环绕速度④环绕速度和质量（　　）
A．①或③
B．①或④
C．②或③
D．②或④

参考答案：研究卫星绕天体做匀速圆周运动，根据万有引力提供向心力，列出等式
GMmr2=m?4π2rT2
M=4π2r3GT2，T为运转周期，r为轨道半径．故①正确．
研究卫星绕天体做匀速圆周运动，根据万有引力提供向心力，列出等式
GMmr2=mv2r
M=rv2G，r为轨道半径，v是环绕速度，故③正确．
在中心体质量的表达式中我们可以发现中心体质量与环绕体质量无关．
故选A．

本题解析：

本题难度：简单

5、填空题  卡文迪许把他自己的实验说成是“称地球的重量”（严格地说应是“测量地球的质量”）。如果已知引力常量G、地球半径R和重力加速度g，那么我们就可以计算出地球的质量M=?；如果已知某行星绕太阳运行所需的向心力是由太阳对该行星的万有引力提供的，该行星做匀速圆周运动，只要测出?和?就可以计算出太阳的质量。

参考答案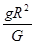：；?行星的公转周期T；?行星距太阳的距离r

本题解析：在地球表面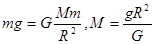?，环绕太阳运行的行星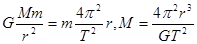，由此可知只要测出行星的公转周期T和行星距太阳的距离r就可以计算出太阳的质量
点评：本题难度较小，在星球表面重力与万有引力相等，这是常用于测量星球质量或表面加速度的方法

本题难度：一般