1、填空题  物体做初速度为零的匀加速直线运动，时间t内位移为x，把位移x分成三段，若通过这三段的时间相等，则这三段的位移大小之比为 1:3:5；若把这段位移分成三等分，则依次通过这三段的时间之比为?。

参考答案：1：3：5?

本题解析：设物体在相等时间段内三段位移的位移分别为x1、x2、x3。 则根据匀变速直线运动推论得 x1：x2：x3=1：3：5
根据初速度为0的匀加速直线运动规律，物体在开始连续通过相等位移的时间比为：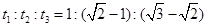

本题难度：一般

2、选择题  （12分）如图所示，倾角为θ的斜面体固定在水平面上，物体的质量为m，物体与斜面之间光滑。物体在沿斜面向上的拉力F作用下，由静止向上运动一段时间后撤去拉力，又经相同时间物体恰滑回原来静止位置。重力加速度大小为g，求拉力F的大小。

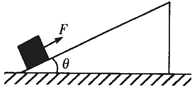
参考答案：

本题解析：有力F作用时，根据牛顿第二定律有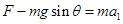?(2分)
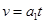根据运动学公式有?(2分)??(2分)
撤去力F后，根据牛顿第二定律有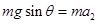?(2分)
根据运动学公式有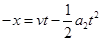?(2分)
联立解得?(2分)．．．

本题难度：一般

3、选择题  一物体做匀变速直线运动，某时刻速度的大小为4m /s，1s后速度的大小变为6m/s．则在这1s内该物体运动的（　　）
A．位移的大小可能小于4m
B．位移的大小可能大于4m
C．路程可能小于5m
D．路程可能大于5m

参考答案：若速度同向，则由v=v0+at可得：a=6-41=2m/s2；物体的位移x=v0t+12at2=4×1+12×2×1=5m；故B正确；
若1s后速度反向，则a′=-6-41m/s2=-10m/s2；1s后的位移x′=v0t+12at2=4×1-12×10×1=-1m；故位移的大小小于4m，故A正确
物体减速到零经过的位移2a′x1=0-v12解得减速过程的位移为0.8m；由v=at可得，减速的时间为410s，反向加速后经过的时间为0.6s，则物体通过的路程等于x2=12×10×（0.6）2=1.8m；总路程为1.8+0.8=2.6m＜5m；故路程不可能大于5m．故C正确，D错误；
故选ABC．

本题解析：

本题难度：简单

4、简答题  有一质量为10千克的木箱静止在水平面上，木箱与水平地面间的摩擦系数为0.5，用绳子沿与水平成37°角的方向拉木箱前进，绳子的拉力F是100牛，拉木箱前进S1=3m时，若突然松手，则松手后木箱还能运动的位移为多大？现有某同学的解法如下：
拉力F拉木箱前进：Fcosθ=100×0.8=80N
f=μmg=0.5×100=50
Fcosθ-f=ma1
a1=（?Fcosθ-f）/m
=[100×0.8-50]/10=（80-50）/10=3?（m/s2）
V12=2a1?S1V1=（2a1?S）1/2=（2×3×3）1/2=4.2（m/s）
突然松手：只有摩擦力产生加速度：
f=ma2即?μmg=ma2a2=μg=0.5×10=5（m/s2）
V12=2a2?S2?S2=V12/2a2=18/（2×5）=1.8（m）
试判断上述解法是否有误，若有错误之处请加以改正并算出正确的结果．

参考答案：松手前对木箱进行受力分析，根据牛顿第二定律得：
a1=Fcosθ-μ(mg-Fsinθ)m=6m/s2
设松手时的速度为v，则有：2a1s1=v2①
突然松手：只有摩擦力产生加速度：
f=ma2即?μmg=ma2
a2=μg=0.5×10=5（m/s2）②
v2=2a2S2?③
由①②③解得：s2=3.6m
所以上述解法是错误的，松手后木箱还能运动的位移为3.6m

本题解析：

本题难度：一般

5、选择题  一物体做加速直线运动，依次通过A、B、C三点，AB=BC。物体在AB段加速度为a1，在BC段加速度为a2，且物体在B点的速度与A、 C两点速度的关系为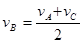，则   （   ）
A．a1> a2        B．a1= a2       C．a1< a2       D．不能确定

参考答案：C

本题解析：考点：匀变速直线运动的速度与时间的关系；匀变速直线运动的位移与时间的关系．
专题：直线运动规律专题．
分析：分别对AB、BC两段运动用位移-速度公式列出方程，结合vB=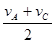即可求解．
解答：解：设AB=BC=x，对AB段有：2a1x=vB2-vA2，解得：a1=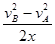
对BC段有：2a2x=vC2-vB2
解得：a1=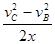，所以a1-a2=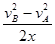-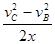又因为vB=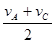
所以a1-a2=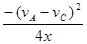，因为物体做加速直线运动，所以vC＞vA
故a1-a2＜0，即a1＜a2
故选C．
点评：该题主要考查了匀加速运动速度-位移公式的直接应用，计算时对同学们的数学功底要求较高，难度适中．

本题难度：一般